
分析 (Ⅰ)根據正弦定理與等比數列的定義,得出sinAsinC=sin2B;
再利用三角恒等變換計算$\frac{1}{tanA}$+$\frac{1}{tanC}$的值;
(Ⅱ)利用正弦、余弦定理求出三角形的面積和a+c的值.
解答 解:(Ⅰ)△ABC中,$sinB=\frac{5}{13}$,且a,b,c成等比數列,
∴ac=b2,
即sinAsinC=sin2B=$\frac{25}{169}$;
∴$\frac{1}{tanA}$+$\frac{1}{tanC}$=$\frac{cosA}{sinA}$+$\frac{cosC}{sinC}$
=$\frac{sinCcosA+cosCsinA}{sinAsinC}$
=$\frac{sin(A+C)}{sinAsinC}$
=$\frac{sinB}{sinAsinC}$
=$\frac{\frac{5}{13}}{\frac{25}{169}}$
=$\frac{13}{5}$;
(Ⅱ)由accosB=12知cosB>0,
由sinB=$\frac{5}{13}$,得cosB=±$\frac{12}{13}$,(舍去負值)
從而b2=ac=$\frac{12}{cosB}$=13;
∴S△ABC=$\frac{1}{2}$acsinB=$\frac{1}{2}$×13×$\frac{5}{13}$=$\frac{5}{2}$;
由余弦定理,得
b2=(a+c)2-2ac-2accosB,
代入數值,得
13=(a+c)2-2×13×(1+$\frac{12}{13}$),
解得:a+c=3$\sqrt{7}$.
點評 本題考查了三角恒等變換與正弦、余弦定理的應用問題,是綜合性題目.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
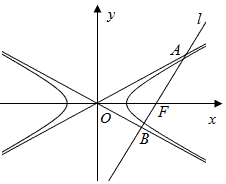 如圖所示,已知雙曲線$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦點為F,過F的直線l交雙曲線的漸近線于A,B兩點,且直線l的傾斜角是漸近線OA傾斜角的2倍,若$\overrightarrow{AF}=2\overrightarrow{FB}$,則該雙曲線的離心率為$\frac{2\sqrt{3}}{3}$.
如圖所示,已知雙曲線$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦點為F,過F的直線l交雙曲線的漸近線于A,B兩點,且直線l的傾斜角是漸近線OA傾斜角的2倍,若$\overrightarrow{AF}=2\overrightarrow{FB}$,則該雙曲線的離心率為$\frac{2\sqrt{3}}{3}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{24}{25}$ | B. | -$\frac{16}{25}$ | C. | $\frac{24}{25}$ | D. | $\frac{12}{25}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -3 | B. | 3 | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-$\frac{π}{2}$,$\frac{π}{2}$) | B. | (-π,-$\frac{π}{2}$) | C. | ($\frac{π}{2}$,π) | D. | ($\frac{3π}{2}$,2π) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com