
分析 (1)根據(jù)條件可求得$\overrightarrow{a}•\overrightarrow{b}=2\sqrt{2}|\overrightarrow{b}|$,進(jìn)行數(shù)量積的運(yùn)算,便可由$(\frac{1}{2}\overrightarrow{a}+\overrightarrow{b})•(2\overrightarrow{a}-3\overrightarrow{b})=12$得出$3|\overrightarrow{b}{|}^{2}-\sqrt{2}|\overrightarrow{b}|-4=0$,解該方程即可求得$|\overrightarrow{b}|$的值;
(2)根據(jù)投影的計(jì)算公式即可得出$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影.
解答 解:(1)根據(jù)條件,$\overrightarrow{a}•\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos45°=2\sqrt{2}|\overrightarrow{b}|$;
∴$(\frac{1}{2}\overrightarrow{a}+\overrightarrow{b})•(2\overrightarrow{a}-3\overrightarrow{b})$=${\overrightarrow{a}}^{2}+\frac{1}{2}\overrightarrow{a}•\overrightarrow{b}-3{\overrightarrow{b}}^{2}$=$16+\sqrt{2}|\overrightarrow{b}|-3|\overrightarrow{b}{|}^{2}=12$;
∴$3|\overrightarrow{b}{|}^{2}-\sqrt{2}|\overrightarrow{b}|-4=0$;
解得$|\overrightarrow{b}|=\sqrt{2}$或$-\frac{2\sqrt{2}}{3}$(舍去);
(2)$\overrightarrow{b}$在$\overrightarrow{a}$上的投影為$|\overrightarrow{b}|cos45°=\sqrt{2}×\frac{\sqrt{2}}{2}=1$.
點(diǎn)評(píng) 考查數(shù)量積的運(yùn)算及計(jì)算公式,一元二次方程的解法,以及投影的定義及計(jì)算公式.


 閱讀快車系列答案
閱讀快車系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
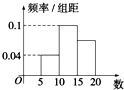
| A. | 12.5、12.5 | B. | 12.5、13 | C. | 13、12.5 | D. | 13、13 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
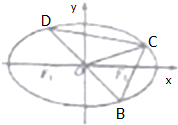 已知橢圓$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>0,b>0})$的兩焦點(diǎn)與短軸的一個(gè)端點(diǎn)的連線構(gòu)成等邊三角形,直線$x+y+2\sqrt{2}-1=0$與以橢圓C的右焦點(diǎn)為圓心,以橢圓的長(zhǎng)半軸長(zhǎng)為半徑的圓相切.
已知橢圓$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>0,b>0})$的兩焦點(diǎn)與短軸的一個(gè)端點(diǎn)的連線構(gòu)成等邊三角形,直線$x+y+2\sqrt{2}-1=0$與以橢圓C的右焦點(diǎn)為圓心,以橢圓的長(zhǎng)半軸長(zhǎng)為半徑的圓相切.查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 36種 | B. | 60種 | C. | 90種 | D. | 120種 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com