
分析 設切點為(${x}_{0},{{x}_{0}}^{3}-2{x}_{0}$),利用導數的幾何意義,求得切線的斜率k=f′(x0),利用點斜式寫出切線方程,將點(1,m)代入切線方程,可得關于x0的方程有三個不同的解,利用參變量分離可得2$2{{x}_{0}}^{3}-3{{x}_{0}}^{2}=-2-m$,令g(x)=2x3-3x2,利用導數求出g(x)的單調性和極值,則根據y=g(x)與y=-2-m有三個不同的交點,即可得到m的取值范圍.
解答 解:設切點為(${x}_{0},{{x}_{0}}^{3}-2{x}_{0}$),
由f(x)=x3-2x,得f′(x)=3x2-2,
∴$f′({x}_{0})=3{{x}_{0}}^{2}-2$.
則切線方程為$y-{{x}_{0}}^{3}+2{x}_{0}=(3{{x}_{0}}^{2}-2)(x-{x}_{0})$.
把(1,m)代入,可得m=$-2{{x}_{0}}^{3}+3{{x}_{0}}^{2}-2$.
∵過點A(1,m)(m≠-2)可作曲線y=f(x)的三條切線,
∴方程m=$-2{{x}_{0}}^{3}+3{{x}_{0}}^{2}-2$有三個不同的根,
令g(x)=2x3-3x2,
∴g′(x)=6x2-6x=0,解得x=0或x=1,
當x<0時,g′(x)>0,當0<x<1時,g′(x)<0,當x>1時,g′(x)>0,
∴g(x)在(-∞,0)上單調遞增,在(0,1)上單調遞減,在(1,+∞)上單調遞增,
∴當x=0時,g(x)取得極大值g(0)=0,
當x=1時,g(x)取得極小值g(1)=-1,
關于x0的方程m=$-2{{x}_{0}}^{3}+3{{x}_{0}}^{2}-2$有三個不同的根,
等價于y=g(x)與y=-2-m的圖象有三個不同的交點,
∴-1<-2-m<0,
∴-2<m<-1,
∴實數m的取值范圍為(-2,-1).
故答案為:(-2,-1).
點評 本題考查了利用導數研究曲線上某點切線方程.導數的幾何意義即在某點處的導數即該點處切線的斜率,解題時要注意運用切點在曲線上和切點在切線上.運用了轉化的數學思想方法,對能力要求較高.屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
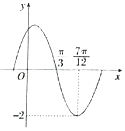 函數f(x)=Asin(ωx+φ)(A,ω,φ是常數,A>0,ω>0)的部分圖象如圖所示,則下列結論:①將f(x)的圖象向左平移$\frac{π}{6}$個單位,所得到的函數是偶函數:②f(0)=1;③最小正周期為π;④$f(\frac{12π}{11})<f(\frac{14π}{13})$;⑤$f(x)=-f(\frac{5π}{3}-x)$.其中正確的結論有( )
函數f(x)=Asin(ωx+φ)(A,ω,φ是常數,A>0,ω>0)的部分圖象如圖所示,則下列結論:①將f(x)的圖象向左平移$\frac{π}{6}$個單位,所得到的函數是偶函數:②f(0)=1;③最小正周期為π;④$f(\frac{12π}{11})<f(\frac{14π}{13})$;⑤$f(x)=-f(\frac{5π}{3}-x)$.其中正確的結論有( )| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [-2,2] | B. | [2,+∞) | C. | [0,+∞) | D. | (-∞,-2]∪[2,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,-2)∪(2,+∞) | B. | (-∞,-2)∪(0,2) | C. | (-2,0)∪(0,2) | D. | (-2,0)∪(2,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 一半徑為4m的水輪(如圖),水輪圓心O距離水面2m,已知水輪每分鐘轉動4圈,如果當水輪上點P從水中浮現時(圖中點P0)開始計時.
一半徑為4m的水輪(如圖),水輪圓心O距離水面2m,已知水輪每分鐘轉動4圈,如果當水輪上點P從水中浮現時(圖中點P0)開始計時.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com