
分析 (1)由f′(x)=a(1+x)a-1-a=a[(1+x)a-1-1],當-1<x<0時,f′(x)>0,當x>0,f′(x)<0,f(x)在x=0處取極大值,也是最大值f(0)=1;
(2)①當a,b中有一個大于1時,不妨設a≥1,ab+ba>ab>1,②當a,b均屬于(0,1),設a=$\frac{1}{1+m}$,b=$\frac{1}{1+n}$,(m,n>0),則ab=$(\frac{1}{1+m})^{\frac{1}{1+n}}$=$\frac{1}{(1+m)^{\frac{1}{1+n}}}$≥$\frac{1}{1+\frac{m}{1+n}}$=$\frac{1+n}{1+m+n}$,同理ba≥$\frac{1+m}{1+m+n}$,即可證明ab+ba>1.
解答 解:(1)由f(x)=(1+x)a-ax,求導f′(x)=a(1+x)a-1-a=a[(1+x)a-1-1],
當-1<x<0時,f′(x)>0,當x>0,f′(x)<0,
∴f(x)在x=0處取極大值,也是最大值f(0)=1,
∴f(x)的最大值為1;
(2)證明:①當a,b中有一個大于1時,不妨設a≥1,
ab+ba>ab>1,
②當a,b均屬于(0,1),設a=$\frac{1}{1+m}$,b=$\frac{1}{1+n}$,(m,n>0),
則ab=$(\frac{1}{1+m})^{\frac{1}{1+n}}$=$\frac{1}{(1+m)^{\frac{1}{1+n}}}$≥$\frac{1}{1+\frac{m}{1+n}}$=$\frac{1+n}{1+m+n}$,
同理可知:ba≥$\frac{1+m}{1+m+n}$,
∴ab+ba>$\frac{1+n}{1+m+n}$+$\frac{1+m}{1+m+n}$=$\frac{2+m+n}{1+m+n}$>1,
∴ab+ba>1.
點評 本題考查利用導數求函數的單調性及極值,考查不等式的證明,考查分類討論思想,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
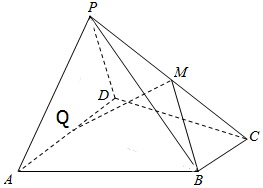 如圖,在四棱錐P-ABCD中,底面ABCD為直角梯形,AD∥BC,∠ADC=90°,Q為AD的中點,M是棱PC的中點,PA=PD=PC,BC=$\frac{1}{2}$AD=2,CD=4
如圖,在四棱錐P-ABCD中,底面ABCD為直角梯形,AD∥BC,∠ADC=90°,Q為AD的中點,M是棱PC的中點,PA=PD=PC,BC=$\frac{1}{2}$AD=2,CD=4查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (2x+2)5 | B. | 2x5 | C. | (2x-1)5 | D. | 32x5 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ①表示無軌跡 ②的軌跡是射線 | B. | ②的軌跡是橢圓 ③的軌跡是雙曲線 | ||
| C. | ①的軌跡是射線④的軌跡是直線 | D. | ②、④均表示無軌跡 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com