
【題目】已知函數f(x)=x2e2x+m|x|ex+1(m∈R)有四個零點,則m的取值范圍為( )
A.(﹣∞,﹣e﹣ ![]() )
)
B.(﹣∞,e+ ![]() )
)
C.(﹣e﹣ ![]() ,﹣2)
,﹣2)
D.(﹣∞,﹣ ![]() )
)
【答案】A
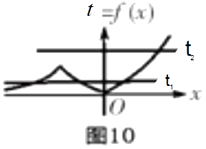
【解析】解:令y=xex , 則y'=(1+x)ex , 由y'=0,得x=﹣1, 當x∈(﹣∞,﹣1)時,y'<0,函數y單調遞減,
當x∈(﹣1,+∞)時,y'>0,函
數y單調遞增.作出y=xex圖象,
利用圖象變換得f(x)=|xex|圖象(如圖10),
令f(x)=t,則關于t方程h(t)=t2+mt+1=0兩根分別在 ![]() 時(如圖11),
時(如圖11),
滿足g(x)=﹣1的x有4個,由 ![]() ,
,
解得m<﹣e﹣ ![]() .
.
故選:A.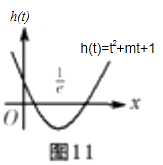
【考點精析】本題主要考查了利用導數研究函數的單調性的相關知識點,需要掌握一般的,函數的單調性與其導數的正負有如下關系: 在某個區(qū)間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區(qū)間單調遞增;(2)如果
在這個區(qū)間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區(qū)間單調遞減才能正確解答此題.
在這個區(qū)間單調遞減才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】設橢圓 ![]() 1(a>
1(a> ![]() )的右焦點為F,右頂點為A,已知
)的右焦點為F,右頂點為A,已知 ![]() ,其中O為原點,e為橢圓的離心率.
,其中O為原點,e為橢圓的離心率.
(1)求橢圓的方程;
(2)設過點A的直線l與橢圓交于B(B不在x軸上),垂直于l的直線與l交于點M,與y軸交于點H,若BF⊥HF,且∠MOA=∠MAO,求直線l的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某賽季甲、乙兩名籃球運動員每場比賽得分的莖葉圖如圖所示,考慮以下結論:
甲 | 乙 | ||||||||
8 | 0 | ||||||||
4 3 3 | 6 6 8 | 3 8 9 1 | 1 2 3 4 5 | 2 5 1 4 0 | 5 4 6 9 | 1 | 6 | 7 | 9 |
①甲運動員得分的中位數大于乙運動員
得分的中位數;
②甲運動員得分的中位數小于乙運動員
得分的中位數;
③甲運動員得分的標準差大于乙運動員
得分的標準差;
④甲運動員得分的標準差小于乙運動員
得分的標準差;
其中根據莖葉圖能得到的正確結論的編號為( )
A. ①③ B. ①④
C. ②③ D. ②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知長方形ABCD中,AB=2AD,M為DC的中點,將△ADM沿AM折起,使得平面ADM⊥平面ABCM. 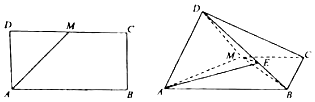
(1)求證:AD⊥BM;
(2)若 ![]() =2
=2 ![]() ,求二面角E﹣AM﹣D的正弦值.
,求二面角E﹣AM﹣D的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《數學九章》中對已知三角形三邊長求三角形的面積的求法填補了我國傳統(tǒng)數學的一個空白,與著名的海倫公式完全等價,由此可以看出我國古代已具有很高的數學水平,其求法是:“以小斜冪并大斜冪減中斜冪,余半之,自乘于上.以小斜冪乘大斜冪減上,余四約之,為實.一為從隔,開平方得積.”若把以上這段文字寫成公式,即S= ![]() .現有周長為2
.現有周長為2 ![]() +
+ ![]() 的△ABC滿足sinA:sinB:sinC=(
的△ABC滿足sinA:sinB:sinC=( ![]() ﹣1):
﹣1): ![]() :(
:( ![]() +1),試用以上給出的公式求得△ABC的面積為( )
+1),試用以上給出的公式求得△ABC的面積為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數![]() 在同一個周期內,當
在同一個周期內,當![]() 時y取最大值1,當
時y取最大值1,當![]() 時,y取最小值﹣1.
時,y取最小值﹣1.
(1)求函數的解析式y=f(x);
(2)函數y=sinx的圖象經過怎樣的變換可得到y=f(x)的圖象?
(3)若函數f(x)滿足方程f(x)=a(0<a<1),求在[0,2π]內的所有實數根之和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓與雙曲線有相同的焦點![]() ,
,![]() ,橢圓的一個短軸端點為
,橢圓的一個短軸端點為![]() ,直線
,直線![]() 與雙曲線的一條漸近線平行,若橢圓于雙曲線的離心率分別為
與雙曲線的一條漸近線平行,若橢圓于雙曲線的離心率分別為![]() ,
,![]() ,則
,則![]() 的最小值為__________.
的最小值為__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com