
【題目】函數![]() 在同一個周期內,當
在同一個周期內,當![]() 時y取最大值1,當
時y取最大值1,當![]() 時,y取最小值﹣1.
時,y取最小值﹣1.
(1)求函數的解析式y=f(x);
(2)函數y=sinx的圖象經過怎樣的變換可得到y=f(x)的圖象?
(3)若函數f(x)滿足方程f(x)=a(0<a<1),求在[0,2π]內的所有實數根之和.
【答案】(1)![]() ;(2)見解析;(3)
;(2)見解析;(3)![]() .
.
【解析】
(1)通過同一個周期內,當![]() 時y取最大值1,當
時y取最大值1,當![]() 時,y取最小值﹣1.求出函數的周期,利用最值求出φ,即可求函數的解析式y=f(x);
時,y取最小值﹣1.求出函數的周期,利用最值求出φ,即可求函數的解析式y=f(x);
(2)函數y=sinx的圖象經過左右平移,然后是橫坐標變伸縮變換,縱坐標不變,可得到y=f(x)的圖象,確定函數解析式;
(3)確定函數在[0,2π]內的周期的個數,利用f(x)=a(0<a<1)與函數的對稱軸的關系,求出所有實數根之和.
(1)∵![]() ,∴
,∴![]() ,
,
又因![]() ,∴
,∴![]() ,又
,又![]() ,得
,得![]()
∴函數![]() ;
;
(2)y=sinx的圖象向右平移![]() 個單位得
個單位得![]() 的圖象,
的圖象,
再由![]() 圖象上所有點的橫坐標變為原來的
圖象上所有點的橫坐標變為原來的![]() .
.
縱坐標不變,得到![]() 的圖象,
的圖象,
∵![]() 的周期為
的周期為![]() ,
,
∴![]() 在[0,2π]內恰有3個周期,
在[0,2π]內恰有3個周期,
∴![]() 在[0,2π]內有6個實根且
在[0,2π]內有6個實根且![]() ,
,
同理,![]() ,
,
故所有實數之和為![]() .
.


科目:高中數學 來源: 題型:
【題目】設f(x)=xlnx﹣ax2+(2a﹣1)x,a∈R.
(1)令g(x)=f′(x),求g(x)的單調區間;
(2)已知f(x)在x=1處取得極大值,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2e2x+m|x|ex+1(m∈R)有四個零點,則m的取值范圍為( )
A.(﹣∞,﹣e﹣ ![]() )
)
B.(﹣∞,e+ ![]() )
)
C.(﹣e﹣ ![]() ,﹣2)
,﹣2)
D.(﹣∞,﹣ ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= 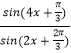 的圖象與g(x)的圖象關于直線x=
的圖象與g(x)的圖象關于直線x= ![]() 對稱,則g(x)的圖象的一個對稱中心為( )
對稱,則g(x)的圖象的一個對稱中心為( )
A.( ![]() ,0)
,0)
B.( ![]() ,0)
,0)
C.( ![]() ,0)
,0)
D.( ![]() ,0)
,0)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 分別為橢圓
分別為橢圓![]() 的左右兩個焦點.
的左右兩個焦點.
(1)若橢圓![]() 上的點
上的點![]() 到
到![]() 兩點的距離之和等于4,寫出橢圓
兩點的距離之和等于4,寫出橢圓![]() 的方程和焦點坐標;
的方程和焦點坐標;
(2)設點![]() 是(1)中所得橢圓上的動點,求線段
是(1)中所得橢圓上的動點,求線段![]() 的中點的軌跡方程;
的中點的軌跡方程;
(3)已知橢圓具有性質:如果![]() 是橢圓
是橢圓![]() 上關于原點對稱的兩個點,點
上關于原點對稱的兩個點,點![]() 是橢圓上任意一點,當直線
是橢圓上任意一點,當直線![]() 的斜率都存在,并記為
的斜率都存在,并記為![]() 時,那么
時,那么![]() 與
與![]() 之積是與點
之積是與點![]() 位置無關的定值,請給予證明.
位置無關的定值,請給予證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x﹣a|,g(x)=x2+2ax+1(a為正實數),滿足f(0)=g(0);
函數F(x)=f(x)+g(x)+b定義域為D.
(1)求a的值;
(2)若存在x0∈D,使F(x0)=x0成立,求實數b的取值范圍;
(3)若n為正整數,證明:![]() <4.
<4.
(參考數據:lg3=0.3010, ![]() =0.1342,
=0.1342,![]() =0.0281,
=0.0281,![]() =0.0038)
=0.0038)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有下列說法:①若![]() ,
,![]() ,則
,則![]() ;②若2
;②若2![]() =
=![]() ,
,![]() 分別表示
分別表示![]() 的面積,則
的面積,則![]() ;③兩個非零向量
;③兩個非零向量![]() ,若|
,若|![]() |=|
|=|![]() |+|
|+|![]() |,則
|,則![]() 與
與![]() 共線且反向;④若
共線且反向;④若![]() ,則存在唯一實數
,則存在唯一實數![]() 使得
使得![]() ,其中正確的說法個數為()
,其中正確的說法個數為()
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2+|x|﹣|x﹣5|+2.
(1)求不等式f(x)<0的解集;
(2)若關于x的不等式|f(x)|≤m的整數解僅有11個,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨機擲兩枚質地均勻的骰子,它們向上的點數之和不超過5的概率記為p1,點數之和大于5的概率記為p2,點數之和為偶數的概率記為p3,則( )
A. p1<p2<p3 B. p2<p1<p3
C. p1<p3<p2 D. p3<p1<p2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com