
分析 (1)利用x=ρcosθ,y=ρsinθ,即可得出M的直角坐標方程;利用直線l過點(1,0)且傾斜角為α,可得直線l的參數方程;
(2)設直線方程為y=k(x-1),代入y2=-4x,可得k2x2-(2k2-4)x+k2=0,分類討論,利用直線l與曲線M只有一個公共點,求傾斜角α的值.
解答 解:(1)x=ρcosθ,y=ρsinθ,
由ρsin2θ+4cosθ=0得ρ2sin2θ=-4ρcosθ.
∴y2=-4x即為曲線M的直角坐標方程;
直線l過點(1,0)且傾斜角為α,故直線l的參數方程為$\left\{\begin{array}{l}{x=1+tcosα}\\{y=tsinα}\end{array}\right.$(t為參數);
(2)設直線方程為y=k(x-1),代入y2=-4x,可得k2x2-(2k2-4)x+k2=0
①k=0,y=0,滿足題意,α=0;
②$\left\{\begin{array}{l}{k≠0}\\{(2{k}^{2}-4)^{2}-4{k}^{4}=0}\end{array}\right.$,∴k=±1,∴α=$\frac{π}{4}$或$\frac{3π}{4}$.
點評 本題考查了極坐標方程化為直角坐標方程、直線參數方程,考查直線與拋物線的位置關系,考查了推理能力與計算能力,屬于中檔題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {1} | B. | (0,1] | C. | [1,+∞) | D. | $[{\frac{1}{2},1}]$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
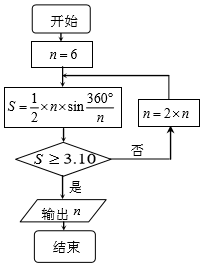 公元263年左右,我國數學家劉徽發現當圓內接正多邊形的邊數無限增加時,多邊形面積可無限逼近圓的面積,并創立了“割圓術”,利用“割圓術”劉徽得到了圓周率精確到小數點后兩位的近似值3.14,就是著名的“徽率”.如圖是利用劉徽的“割圓術”思想設計的一個程序框圖,則輸出的值為( )(參考數據:sin15°=0.2588,sin7.5°=0.1305)
公元263年左右,我國數學家劉徽發現當圓內接正多邊形的邊數無限增加時,多邊形面積可無限逼近圓的面積,并創立了“割圓術”,利用“割圓術”劉徽得到了圓周率精確到小數點后兩位的近似值3.14,就是著名的“徽率”.如圖是利用劉徽的“割圓術”思想設計的一個程序框圖,則輸出的值為( )(參考數據:sin15°=0.2588,sin7.5°=0.1305)| A. | 22 | B. | 23 | C. | 24 | D. | 25 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-1,3] | B. | (-1,3) | C. | [-3,1) | D. | [-3,1] |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com