Question

4．為了測量兩山頂M、N間的距離，飛機沿水平方向在A、B兩點進行測量．A、B、M、N在同一個鉛垂平面內（如示意圖）．飛機能夠測量的數據有俯角和A、B間的距離．現測得AB間的距離為d，A點到M、N點的俯角為α₁、β₁；B點到M、N點的俯角為α₂、β₂，請將測量所得到的數據在圖上標出，并用所測得的數據、公式和必要的文字寫出M、N間距離的表達式．（用所測得的數據寫出MN的表達式）．

Answer 1

分析 在△ABM和△ABN中利用正弦定理計算BM，BN，在△BMN中利用余弦定理計算MN．

解答 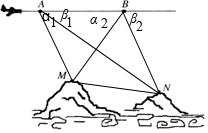解：由題意可知∠BAM=α₁，∠ABM=α₂，AB=d，
則△ABM中，∠AMB=180°-α₁-α₂，
由正弦定理可得$\frac{AB}{sin∠AMB}=\frac{BM}{sin∠BAM}$，即$\fracp9vv5xb5{sin（{α}_{1}+{α}_{2}）}$=$\frac{BM}{sin{α}_{1}}$，
∴BM=$\frac{dsin{α}_{1}}{sin（{α}_{1}+{α}_{2}）}$，
在△ABN中，∠ANB=β₂-β₁，
由正弦定理得$\frac{BN}{sin∠BAN}=\frac{AB}{sin∠ANB}$，即$\fracp9vv5xb5{sin（{β}_{2}-{β}_{1}）}$=$\frac{BN}{sin{β}_{1}}$，
∴BN=$\frac{dsin{β}_{1}}{sin（{β}_{2}-{β}_{1}）}$，
在△BMN中，∠MBN=180°-α₂-β₂，∴cos∠MBN=-cos（α₂+β₂），
由余弦定理得MN²=BM²+BN²-2BM•BN•cos∠MBN=$\frac{p9vv5xb5^{2}si{n}^{2}{α}_{1}}{si{n}^{2}（{α}_{1}+{α}_{2}）}$+$\frac{p9vv5xb5^{2}si{n}^{2}{β}_{1}}{si{n}^{2}（{β}_{2}-{β}_{1}）}$+$\frac{{2d}^{2}sin{α}_{1}sin{β}_{1}cos（{α}_{2}+{β}_{2}）}{sin（{α}_{1}+{α}_{2}）sin（{β}_{2}-{β}_{1}）}$，
∴MN=d$\sqrt{\frac{si{n}^{2}{α}_{1}}{si{n}^{2}（{α}_{1}+{α}_{2}）}+\frac{si{n}^{2}{β}_{1}}{si{n}^{2}（{β}_{2}-{β}_{1}）}+\frac{2sin{α}_{1}sin{β}_{1}cos（{α}_{2}+{β}_{2}）}{sin（{α}_{1}+{α}_{2}）sin（{β}_{2}-{β}_{1}）}}$，

點評 本題考查了正余弦定理在解三角形中的應用，屬于中檔題．