
分析 (Ⅰ)通過討論x的范圍,求出各個區間上的不等式的解集,取并集即可;
(Ⅱ)通過討論a的范圍,求出各個區間上的函數的最小值,得到關于a的方程,解出即可.
解答 解:(Ⅰ)a=1時,f(x)=|x+1|+2|x-1|,
x≥1時,f(x)=x+1+2x-2=3x-1>2,解得:x>1,
-1<x<1時,f(x)=x+1+2-2x=-x+3>2,解得:x<1,
x≤-1時,f(x)=-x-1+2-2x=-3x+1>2,解得:x<-$\frac{1}{3}$,
綜上,不等式的解集是(-∞,1)∪(1,+∞);
(II) ①a>-1時,
x≥a時,f(x)=x+1+2x-2a=3x+1-2a,
此時,f(x)min=f(a)=a+1,
-1≤x≤a時,f(x)=x+1+2a-2x=-x+2a+1,
此時,f(x)min=f(a)=a+1;
x≤-1時,f(x)=-x-1+2a-2x=-3x+2a-1,
此時,f(x)min=f(-1)=2a+2,
由a>-1,得2a+2>a+1,
綜上,f(x)的最小值是f(a)=a+1=5,解得:a=4;
②a<-1時,
x≥-1時,f(x)=x+1+2x-2a=3x+1-2a,
此時,f(x)min=f(-1)=-2a-2,
a≤x≤-1時,f(x)=-x-1+2x-2a=x-1-2a,
此時,f(x)min=f(a)=-a-1,
x≤a時,f(x)=-x-1-2x+2a=-3x+2a-1,
此時,f(x)min=f(a)=-a-1,
由a<-1,則-a-1<-2a-2,
故f(x)的最小值是f(a)=-a-1=5,解得:a=-6,
綜合①②a=4或a=-6.
點評 本題考查了解絕對值不等式問題,考查分類討論思想以及函數最值問題,是一道中檔題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 已知空間幾何體CBEADF如圖所示,底面AEFD為矩形,平面BEFC⊥平面AEFD,∠CFE=∠BEF=90°,其中AE+BE=AD=2,DF+CF=4.
已知空間幾何體CBEADF如圖所示,底面AEFD為矩形,平面BEFC⊥平面AEFD,∠CFE=∠BEF=90°,其中AE+BE=AD=2,DF+CF=4.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{7}{16}$ | B. | 7 | C. | 16 | D. | 28 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
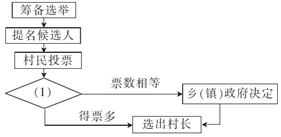 選舉時常用的選舉方式是差額選舉(候選人多于當選人數),某村選舉村長,具體方法是:籌備選舉,由鄉(鎮)政府提名候選人,村民投票(同意,不同意,棄權),驗票統計,得票多者選為村長;若票數相等,則由鄉(鎮)政府決定誰當選.下面的流程圖表示該選舉過程,則圖(1)處應填的是驗票統計.
選舉時常用的選舉方式是差額選舉(候選人多于當選人數),某村選舉村長,具體方法是:籌備選舉,由鄉(鎮)政府提名候選人,村民投票(同意,不同意,棄權),驗票統計,得票多者選為村長;若票數相等,則由鄉(鎮)政府決定誰當選.下面的流程圖表示該選舉過程,則圖(1)處應填的是驗票統計.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com