
分析 運用向量的投影定義,可得|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=2,再由cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$,計算即可得到所求夾角.
解答 解:$\overrightarrow a•\overrightarrow b=4\sqrt{3}$,
若$\overrightarrow a$在$\overrightarrow b$方向上投影為$2\sqrt{3}$,$\overrightarrow b$在$\overrightarrow a$方向上的投影為$\sqrt{3}$,
可得$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{b}|}$=2$\sqrt{3}$,$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|}$=$\sqrt{3}$,
即有|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=2,
則cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$=$\frac{4\sqrt{3}}{4×2}$=$\frac{\sqrt{3}}{2}$,
由0≤<$\overrightarrow{a}$,$\overrightarrow{b}$>≤π,
可得$\overrightarrow a$與$\overrightarrow b$的夾角為$\frac{π}{6}$.
故答案為:$\frac{π}{6}$.
點評 本題考查向量的夾角的求法,注意運用向量的投影概念和向量數量積的夾角公式,考查運算能力,屬于基礎題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:填空題
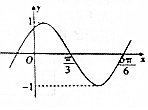 已知函數y=sin(ωx+φ)(ω>0,0<φ≤$\frac{π}{2}$)的部分圖象如圖所示,則cos(5ωφ)=-$\frac{1}{2}$.
已知函數y=sin(ωx+φ)(ω>0,0<φ≤$\frac{π}{2}$)的部分圖象如圖所示,則cos(5ωφ)=-$\frac{1}{2}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | $\frac{4}{5}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com