
(本小題滿分12分)已知函數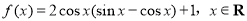 .
.
(1)求函數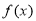 的最小正周期;
的最小正周期;
(2)求函數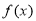 在區間
在區間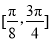 上的最小值和最大值.
上的最小值和最大值.
科目:高中數學 來源:2014-2015學年河南省高二上學期第一次月考試理科數學卷(解析版) 題型:選擇題
在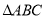 中,若
中,若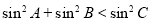 ,則
,則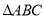 的形狀是 ( )
的形狀是 ( )
A.鈍角三角形 B.直角三角形 C.銳角三角形 D.不能確定
查看答案和解析>>
科目:高中數學 來源:2014-2015學年河北邢臺一中高二上學期期中考試文科數學試卷(解析版) 題型:選擇題
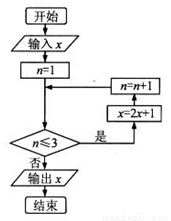
已知實數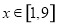 ,執行如圖所示的程序框圖,則輸出的x不小于55的概率為( )
,執行如圖所示的程序框圖,則輸出的x不小于55的概率為( )
A.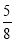 B.
B.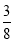 C.
C.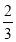 D.
D.
查看答案和解析>>
科目:高中數學 來源:2014-2015學年廣東省山一等七校高三12月聯考文科數學試卷(解析版) 題型:解答題
(本小題滿分14分)已知函數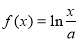 .
.
(1)若曲線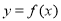 在
在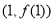 處的切線為
處的切線為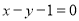 ,求
,求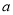 的值;
的值;
(2)設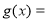
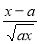 ,
,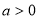 ,證明:當
,證明:當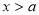 時,
時,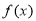 的圖象始終在
的圖象始終在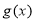 的圖象的下方;
的圖象的下方;
(3)當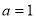 時,設
時,設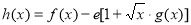 ,(
,(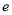 為自然對數的底數),
為自然對數的底數),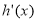 表示
表示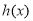 導函數,求證:對于曲線
導函數,求證:對于曲線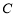 上的不同兩點
上的不同兩點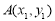 ,
,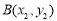 ,
,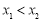 ,存在唯一的
,存在唯一的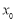
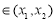 ,使直線
,使直線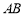 的斜率等于
的斜率等于 .
.
查看答案和解析>>
科目:高中數學 來源:2014-2015學年廣東省山一等七校高三12月聯考文科數學試卷(解析版) 題型:填空題
函數 的圖象中相鄰兩條對稱軸的距離為____________________________.
的圖象中相鄰兩條對稱軸的距離為____________________________.
查看答案和解析>>
科目:高中數學 來源:2014-2015學年廣東省山一等七校高三12月聯考文科數學試卷(解析版) 題型:選擇題
已知實數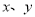 滿足約束條件
滿足約束條件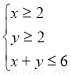 ,則
,則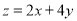 的最大值為( ).
的最大值為( ).
A.24 B.20 C.16 D.12
查看答案和解析>>
科目:高中數學 來源:2014-2015學年廣東省山一等七校高三12月聯考理科數學試卷(解析版) 題型:選擇題
由無理數引發的數學危機一直延續到19世紀.直到1872年,德國數學家戴德金從連續性的要求出發,用有理數的“分割”來定義無理數(史稱戴德金分割),并把實數理論建立在嚴格的科學基礎上,才結束了無理數被認為“無理”的時代,也結束了持續2000多年的數學史上的第一次大危機.所謂戴德金分割,是指將有理數集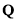 劃分為兩個非空的子集
劃分為兩個非空的子集 與
與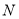 ,且滿足
,且滿足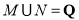 ,
,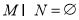 ,
, 中的每一個元素都小于
中的每一個元素都小于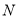 中的每一個元素,則稱
中的每一個元素,則稱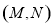 為戴德金分割.試判斷,對于任一戴德金分割
為戴德金分割.試判斷,對于任一戴德金分割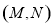 ,下列選項中,不可能成立的是( )
,下列選項中,不可能成立的是( )
A. 沒有最大元素,
沒有最大元素,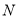 有一個最小元素
有一個最小元素
B. 沒有最大元素,
沒有最大元素,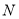 也沒有最小元素
也沒有最小元素
C. 有一個最大元素,
有一個最大元素,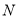 有一個最小元素
有一個最小元素
D. 有一個最大元素,
有一個最大元素,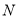 沒有最小元素
沒有最小元素
查看答案和解析>>
科目:高中數學 來源:2014-2015學年廣東省肇慶市畢業班第一次統一檢測理科數學試卷(解析版) 題型:選擇題
現有16張不同的卡片,其中紅色、黃色、藍色、綠色卡片各4張,從中任取3張,要求這三張卡片不能是同一種顏色,且綠色卡片至多1張,不同的取法的種數為
A.484 B.472 C.252 D.232
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com