
 設函數f(x)=$\frac{b\sqrt{{a}^{2}-{x}^{2}}}{a}$(a>b>0)的圖象是曲線C.
設函數f(x)=$\frac{b\sqrt{{a}^{2}-{x}^{2}}}{a}$(a>b>0)的圖象是曲線C.分析 (1)化簡函數的解析式為$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,a>b>0,且y≥0,其圖象表示焦點在x軸上橢圓的一部分,數形結合求得,A1 和A2的坐標.
(2)先考察一般性,直線A1P的方程是y=k(x+a),與橢圓方程聯立,求得P,Q的坐標,可得直線PQ斜率,即可求出取值范圍.
解答  解:(1)∵f(x)=$\frac{b\sqrt{{a}^{2}-{x}^{2}}}{a}$(a>b>0),
解:(1)∵f(x)=$\frac{b\sqrt{{a}^{2}-{x}^{2}}}{a}$(a>b>0),
∴y=$\frac{b\sqrt{{a}^{2}-{x}^{2}}}{a}$,
∴a2y2=b2(a2-x2),∴b2x2+a2y2=b2a2,
∴$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,a>b>0,且y≥0,
其圖象表示焦點在x軸上橢圓的一部分,
如圖所示,A1 (-a,0)、A2(a,0).
(2)曲線C的方程是$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,y≥0),
設 直線A1P的斜率是k,
因為P是曲線C上位于第一象限內的任意一點,所以k∈(0,$\frac{b}{a}$).
設P,Q的坐標分別是(x1,y1),(x2,y2),則直線A1P的方程是y=k(x+a),
由$\left\{\begin{array}{l}{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\\{y=k(x+a)}\end{array}\right.$消去y得,(a2k2+b2)x2+2a3k2x+a2(a2k2-b2)=0,
解得x1=$\frac{a({b}^{2}-{a}^{2}{k}^{2})}{{b}^{2}+{a}^{2}{k}^{2}}$,y1=$\frac{2a{b}^{2}k}{{b}^{2}+{a}^{2}{k}^{2}}$.
將上式中的a換成-a,k換成-$\frac{1}{k}$得x2=$\frac{a({a}^{2}-{b}^{2}{k}^{2})}{{a}^{2}+{b}^{2}{k}^{2}}$,y2=$\frac{2a{b}^{2}k}{{a}^{2}+{b}^{2}{k}^{2}}$,
∴KPQ=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$=$\frac{1}{3}$(k-$\frac{1}{k}$),由于y=$\frac{1}{3}$(k-$\frac{1}{k}$)在∈(0,$\frac{b}{a}$)上單調遞增,
∴KPQ=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$=$\frac{1}{3}$(k-$\frac{1}{k}$)<$\frac{1}{3}$($\frac{b}{a}$-$\frac{a}{b}$)=$\frac{{b}^{2}{-a}^{2}}{ab}$,
故直線PQ斜率的取值范圍為(-∞,$\frac{{b}^{2}{-a}^{2}}{ab}$).
點評 本題考查橢圓方程,考查直線與橢圓的位置關系,考查斜率的計算,考查學生分析解決問題的能力,屬于難題.


科目:高中數學 來源: 題型:選擇題
| A. | a>c>b | B. | b>c>a | C. | b>a>c | D. | c>b>a |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
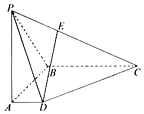 如圖,在四棱錐P-ABCD中,PA⊥底面ABCD,AD∥BC,∠DAB=90°,PA=AB=BC=3,AD=1.
如圖,在四棱錐P-ABCD中,PA⊥底面ABCD,AD∥BC,∠DAB=90°,PA=AB=BC=3,AD=1.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 4 | B. | 2$\sqrt{2}$ | C. | 8 | D. | 與m有關 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (0,$\frac{1}{e}$) | B. | (0,e) | C. | (-∞,$\frac{1}{e}$) | D. | (0,$\frac{1}{e}$] |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 當x>0時,y隨x的增大而增大 | B. | 當x=2時,y有最大值-3 | ||
| C. | 圖象的頂點坐標為(-2,-7) | D. | 圖象與x軸有兩個交點 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com