Question

7．橢圓C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左頂點到右焦點的距離為$\sqrt{3}$+$\sqrt{2}$，橢圓上的點到右焦點的距離的最小值為$\sqrt{3}$-$\sqrt{2}$．
（1）求橢圓C的方程；
（2）設斜率為1的直線l經過橢圓上頂點，并與橢圓交于A，B兩點，求|AB|．

Answer 1

分析 （1）由題意可得a，c的方程組，求解可得a，c的值，結合隱含條件求得b，則橢圓方程可求；
（2）由已知可得直線l的方程，與橢圓方程聯立，可得B的坐標，由|AB|=$\sqrt{2}|{x}_{A}-{x}_{B}|$求得答案．

解答 解：（1）設橢圓$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的半焦距為c，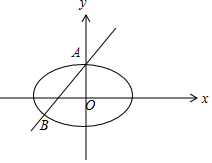
由題意可得：$\left\{\begin{array}{l}{a+c=\sqrt{3}+\sqrt{2}}\\{a-c=\sqrt{3}-\sqrt{2}}\end{array}\right.$，解得a=$\sqrt{3}$，c=$\sqrt{2}$．
∴b²=a²-c²=1．
則橢圓C的方程為$\frac{{x}^{2}}{3}+{y}^{2}=1$；
（2）如圖，橢圓C的上頂點A（0，1），
則直線l的方程y=x+1．
聯立$\left\{\begin{array}{l}{y=x+1}\\{\frac{{x}^{2}}{3}+{y}^{2}=1}\end{array}\right.$，得2x²+3x=0．
解得：${x}_{A}=0，{x}_{B}=-\frac{3}{2}$．
∴|AB|=$\sqrt{2}|{x}_{A}-{x}_{B}|=\frac{3\sqrt{2}}{2}$．

點評 本題考查橢圓的簡單性質，考查直線與橢圓位置關系的應用，明確橢圓上的點中，左頂點到右焦點的距離最大，右頂點到右焦點的距離最小是關鍵，是中檔題．