Question

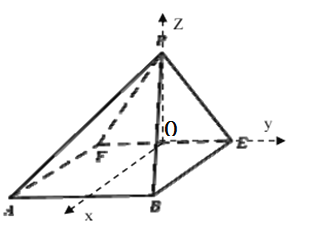
【題目】如圖（1），等腰梯形，，，，、分別是的兩個(gè)三等分點(diǎn).若把等腰梯形沿虛線、折起，使得點(diǎn)和點(diǎn)重合，記為點(diǎn)，如圖（2）.

（1）求證：平面平面；

（2）求平面與平面所成銳二面角的余弦值.

Answer 1

【答案】（1）證明見解析；（2）.

【解析】

（1）根據(jù)線面垂直的判定定理，先證明面，再由面面垂直的判定定理，即可得出結(jié)論成立；

（2）過(guò)作于，過(guò)作BE的平行線交AB于，得到面，又，EF，所在直線兩兩垂直，以它們?yōu)檩S建立空間直角坐標(biāo)系，用空間向量的方法，分別求出平面和平面的法向量，計(jì)算向量夾角余弦值，即可求出結(jié)果.

（1）因?yàn)?/span>，是的兩個(gè)三等分點(diǎn)，易知，是正方形，故，

又，且，所以面，

又面，所以面.

（2）過(guò)作于，過(guò)作BE的平行線交AB于，則面，

又，EF，所在直線兩兩垂直，以它們?yōu)檩S建立空間直角坐標(biāo)系，

則，，，，

所以，，，，

設(shè)平面的法向量為，

則，∴，，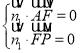

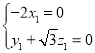設(shè)平面的法向量為，

則，∴，，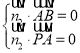

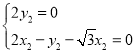因此，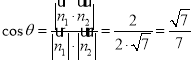

所以平面與平面所成銳二面角的余弦值.