
| A. | 6 | B. | $\frac{15}{2}$ | C. | 10 | D. | 12 |
分析 設(shè)A、B、C所對邊分別為a,b,c,由$\overrightarrow{AB}$•$\overrightarrow{AC}$=5且|$\overrightarrow{AB}$-$\overrightarrow{AC}$|=4,得bccosA=5,a=4,結(jié)合余弦定理可得b2+c2,再由基本不等式可得bc最大值,即可求出△ABC面積的最大值.
解答 解:設(shè)A、B、C所對邊分別為a,b,c,
由$\overrightarrow{AB}$•$\overrightarrow{AC}$=5,|$\overrightarrow{AB}$-$\overrightarrow{AC}$|=4,得bccosA=5,a=4,①
S△ABC=$\frac{1}{2}$bcsinA=$\frac{1}{2}$bc$\sqrt{1-co{s}^{2}A}$=$\frac{1}{2}$bc$•\sqrt{1-\frac{25}{{b}^{2}{c}^{2}}}$=$\frac{1}{2}\sqrt{{b}^{2}{c}^{2}-25}$,
由余弦定理可得b2+c2-2bccosA=16,②
由①②消掉cosA得b2+c2=26,
∴bc≤$\frac{{b}^{2}+{c}^{2}}{2}$=13,當(dāng)且僅當(dāng)b=c=$\frac{13}{2}$時取等號,
∴S△ABC=$\frac{1}{2}$$\sqrt{{b}^{2}{c}^{2}-25}$≤6,
∴△ABC的面積的最大值為6.
故選:A.
點評 本題考查平面向量數(shù)量積的運算、三角形面積公式、基本不等式求最值等知識,綜合性較強,屬中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
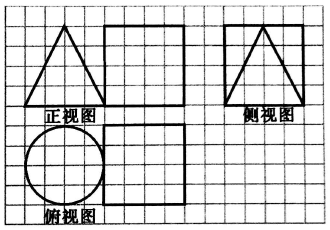
| A. | 4$\sqrt{5}π+96$ | B. | (2$\sqrt{5}+6$)π+96 | C. | (4$\sqrt{5}+4$)π+64 | D. | (4$\sqrt{5}$+4)π+96 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | -2 | B. | -3 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 64 | B. | 80 | C. | 256 | D. | 320 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com