
| A. | f(x)>g(x) | B. | f(x)<g(x) | C. | f(x)+g(b)>g(x)+f(b) | D. | f(x)+g(a)>g(x)+f(a) |
分析 比較大小常用方法就是作差,構造函數F(x)=f(x)-g(x),研究F(x)在給定的區間[a,b]上的單調性,F(x)在給定的區間[a,b]上是增函數從而F(x)>F(a),整理后得到答案.
解答 解:設F(x)=f(x)-g(x),
∵在[a,b]上f'(x)>g'(x),
F′(x)=f′(x)-g′(x)>0,
∴F(x)在給定的區間[a,b]上是增函數.
∴當x>a時,F(x)>F(a),
即f(x)-g(x)>f(a)-g(a)
即f(x)+g(a)>g(x)+f(a)
故選:D.
點評 本題考查的知識點是利用導數研究函數的單調性,其中根據已知條件構造函數F(x)=f(x)-g(x),進而判斷其單調性是解答本題的關鍵.


 新非凡教輔沖刺100分系列答案
新非凡教輔沖刺100分系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{3}$ | B. | 3 | C. | $\sqrt{5}$ | D. | 5 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
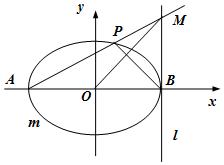 已知橢圓$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的離心率為$\frac{1}{2}$,且過點$E({1,\frac{3}{2}})$.
已知橢圓$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的離心率為$\frac{1}{2}$,且過點$E({1,\frac{3}{2}})$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com