
分析 (1)利用新定義,可以判斷集合M={0,2,4}具有性質P,N={1,2,3}不具有性質P;
(2)根據數列:a1,a2,…an(0≤a1<a2…<an),n≥3時具有性質P,對任意i,j(1≤i<j≤n),aj+ai與aj-ai兩數中至少有一個是該數列中的一項
(3)確定a1=0,再利用新定義,即可判斷具有性質P的集合A中的數列{an}是否一定成等差數列.
解答 (1)解:集合M={0,2,4}具有性質P,N={1,2,3}不具有性質P.
∵集合M={0,2,4}中,aj+ai與aj-ai(1≤i≤j≤2)兩數中都是該數列中的項,4-2是該數列中的項,
∴集合M={0,2,4}具有性質P;
N={1,2,3}中,3在此集合中,則由題意得3+3和3-3至少一個一定在,而3+3=6不在,所以3-3=0一定是這個集合的元素,而此集合沒有0,故不具有性質P;
(2)①數列中的最大項an,顯然an+an=2an不是數列中的項,則必有an-an=0屬于該數列,故0∈A,所以a1=0,
②若數列A具有該性質P,設an是最大項,則具有性質ai+an(1<i≤n,i∈N*),不在A中,則an-ai是數列A中的項,則依題意:an-an<an-an-1<an-an-2<…<an-a2<an-a1,則由給的數列A的性質可知;an-an=a1,an-an-1=a2,an-an-2=a3,…an-a2=an-1,an-a1=an,將前面n個式子相加得:nan-(a1+a2+a3+…an-1+an)=a1+a2+a3+…+an-1+an,故nan=2(a1+a2+a3+…an-1+an),
故a1+a2+a3+…+an=$\frac{n}{2}$an
(3)解:n=3時,∵數列a1,a2,a3具有性質P,0≤a1<a2<a3
∴a2+a3與a3-a2至少有一個是該數列中的一項,
∵a1=0,a2+a3不是該數列的項,∴a3-a2=a2,∴a1+a3=2a2,數列{an}一定成等差數列;
n=4時,∵數列a1,a2,a3,a4具有性質P,0≤a1<a2<a3<a4,
∴a3+a4與a4-a3至少有一個是該數列中的一項,
∵a3+a4不是該數列的項,∴a4-a3=a2,或a4-a3=a3,
若a4-a3=a2,則數列{an}一定成等差數列;若a4-a3=a3,則數列{an}不一定成等差數列;
點評 本題考查數列的綜合應用,考查學生的應用知識分析、解決問題的能力,屬于難題


 口算題天天練系列答案
口算題天天練系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
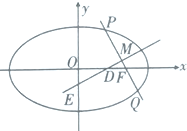 平面直角坐標系的原點為O,橢圓$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的右焦點為F,直線PQ過F交橢圓于P,Q兩點,且|PF|max•|QF|min=$\frac{a^2}{4}$.
平面直角坐標系的原點為O,橢圓$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的右焦點為F,直線PQ過F交橢圓于P,Q兩點,且|PF|max•|QF|min=$\frac{a^2}{4}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
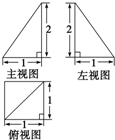
| A. | 2+$\sqrt{5}$ | B. | 3+$\frac{\sqrt{5}}{2}$ | C. | 2+$\frac{\sqrt{5}}{2}$ | D. | 3+$\sqrt{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
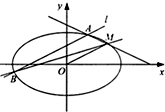 如圖,橢圓C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的虛軸長為2$\sqrt{2}$,點M(2,1)在C上,平行于OM的直線l交橢圓C于不同的兩點A,B.
如圖,橢圓C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的虛軸長為2$\sqrt{2}$,點M(2,1)在C上,平行于OM的直線l交橢圓C于不同的兩點A,B.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (0,2) | B. | [0,2)∪[3,+∞) | C. | [1,+∞) | D. | [2,3] |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-2,2) | B. | (-∞,-2)∪(0,2) | C. | (-∞,-2)∪(2,+∞) | D. | (-2,0)∪(2,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com