
分析 (1)利用組合數的計算公式即可得出.
(2)方法一:由(1)可知當k≥2時${({k+1})^2}C_n^k=({{k^2}+2k+1})C_n^k={k^2}C_n^k+2kC_n^k+C_n^k$=$[{n({n-1})C_{n-2}^{k-2}+nC_{n-1}^{k-1}}]+2nC_{n-1}^{k-1}+C_n^k=n({n-1})C_{n-2}^{k-2}+3nC_{n-1}^{k-1}+C_n^k$.代入化簡即可得出.
方法二:當n≥3時,由二項式定理,有${({1+x})^n}=1+C_n^1x+C_n^2{x^2}+…+C_n^k{x^k}+…+C_n^n{x^n}$,
兩邊同乘以x,得${({1+x})^n}x=x+C_n^1{x^2}+C_n^2{x^3}+…+C_n^k{x^{k+1}}+…+C_n^n{x^{n+1}}$,
兩邊對x求導,得${({1+x})^n}+n{({1+x})^{n-1}}x=1+2C_n^1x+3C_n^2{x^2}+…+({k+1})C_n^k{x^k}+…+({n+1})C_n^n{x^n}$,兩邊再同乘以x,得${({1+x})^n}x+n{({1+x})^{n-1}}{x^2}=x+2C_n^1{x^2}+3C_n^2{x^3}+…+({k+1})C_n^k{x^{k+1}}+…+({n+1})C_n^n{x^{n+1}}$,
兩邊再對x求導,得(1+x)n+n(1+x)n-1x+n(n-1)(1+x)n-2x2+2n(1+x)n-1x=$1+{2^2}C_n^1x+{3^2}C_n^2{x^2}+…+{({k+1})^2}C_n^k{x^k}+…+{({n+1})^2}C_n^n{x^n}$.
令x=1,即可得出.
解答 解:(1)①$kC_n^k-nC_{n-1}^{k-1}=k×\frac{n!}{{k!({n-k})!}}-n×\frac{{({n-1})!}}{{({k-1})!({n-k})!}}$=$\frac{n!}{{({k-1})!({n-k})!}}-\frac{n!}{{({k-1})!({n-k})!}}=0$.…(2分)
②${k^2}C_n^k-n({n-1})C_{n-2}^{k-2}-nC_{n-1}^{k-1}={k^2}×\frac{n!}{{k!({n-k})!}}-n({n-1})×\frac{{({n-2})!}}{{({k-2})!({n-k})!}}$$-n×\frac{{({n-1})!}}{{({k-1})!({n-k})!}}$=$k×\frac{n!}{{({k-1})!({n-k})!}}-\frac{n!}{{({k-2})!({n-k})!}}-\frac{n!}{{({k-1})!({n-k})!}}$=$\frac{n!}{{({k-2})!({n-k})!}}({\frac{k}{k-1}-1-\frac{1}{k-1}})=0$.…(4分)
(2)方法一:由(1)可知當k≥2時${({k+1})^2}C_n^k=({{k^2}+2k+1})C_n^k={k^2}C_n^k+2kC_n^k+C_n^k$=$[{n({n-1})C_{n-2}^{k-2}+nC_{n-1}^{k-1}}]+2nC_{n-1}^{k-1}+C_n^k=n({n-1})C_{n-2}^{k-2}+3nC_{n-1}^{k-1}+C_n^k$.(6分)
故${1^2}C_n^0+{2^2}C_n^1+{3^2}C_n^2+…+{({k+1})^2}C_n^k+…+{({n+1})^2}C_n^n$=$({{1^2}C_n^0+{2^2}C_n^1})+n({n-1})({C_{n-2}^0+C_{n-2}^1+…+C_{n-2}^{n-2}})+3n({C_{n-1}^1+C_{n-1}^2+…+C_{n-1}^{n-1}})$$+({C_n^2+C_n^3+…+C_n^n})$=(1+4n)+n(n-1)2n-2+3n(2n-1-1)+(2n-1-n)=2n-2(n2+5n+4).…(10分)
方法二:當n≥3時,由二項式定理,有${({1+x})^n}=1+C_n^1x+C_n^2{x^2}+…+C_n^k{x^k}+…+C_n^n{x^n}$,
兩邊同乘以x,得${({1+x})^n}x=x+C_n^1{x^2}+C_n^2{x^3}+…+C_n^k{x^{k+1}}+…+C_n^n{x^{n+1}}$,
兩邊對x求導,得${({1+x})^n}+n{({1+x})^{n-1}}x=1+2C_n^1x+3C_n^2{x^2}+…+({k+1})C_n^k{x^k}+…+({n+1})C_n^n{x^n}$,…(6分)
兩邊再同乘以x,得${({1+x})^n}x+n{({1+x})^{n-1}}{x^2}=x+2C_n^1{x^2}+3C_n^2{x^3}+…+({k+1})C_n^k{x^{k+1}}+…+({n+1})C_n^n{x^{n+1}}$,
兩邊再對x求導,得(1+x)n+n(1+x)n-1x+n(n-1)(1+x)n-2x2+2n(1+x)n-1x=$1+{2^2}C_n^1x+{3^2}C_n^2{x^2}+…+{({k+1})^2}C_n^k{x^k}+…+{({n+1})^2}C_n^n{x^n}$.…(8分)
令x=1,得2n+n2n-1+n(n-1)2n-2+2n2n-1=$1+{2^2}C_n^1+{3^2}C_n^2+…+{({k+1})^2}C_n^k+…+{({n+1})^2}C_n^n$,
即${1^2}C_n^0+{2^2}C_n^1+{3^2}C_n^2+…+{({k+1})^2}C_n^k+…+{({n+1})^2}C_n^n$=2n-2(n2+5n+4).…(10分)
點評 本題考查了組合數的計算公式及其性質、利用導數的運算法則化簡證明,考查了推理能力與計算能力,屬于中檔題.


科目:高中數學 來源: 題型:解答題
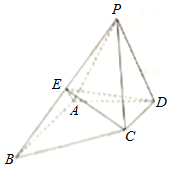 如圖,四棱錐P-ABCD中,△PAD為正三角形,AB∥CD,AB=2CD,∠BAD=90°,PA⊥CD,E為棱PB的中點
如圖,四棱錐P-ABCD中,△PAD為正三角形,AB∥CD,AB=2CD,∠BAD=90°,PA⊥CD,E為棱PB的中點查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (1,2) | B. | (2,+∞) | C. | $(1,\;\sqrt{2})$ | D. | $(\sqrt{2},\;+∞)$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {a|a>2} | B. | {a|1<a<2} | C. | $\{a|a>\frac{1}{2}\}$ | D. | $\{a|\frac{1}{2}<a<1\}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ∅ | B. | {2} | C. | {2,3} | D. | {x|2≤x<3} |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com