
分析 (1)把m,n的值代入函數解析式,求出原函數的導函數,得到導函數的零點,從而求得原函數的極值點,求出極值;
(2)把n=-1代入函數解析式,求出導函數,由函數的單調性求得f(x)在[1,4]上的最大值為f(4)=8m+$\frac{40}{3}=\frac{16}{3}$.求得m值,進一步求出函數在區間[1,4]上的最小值.
解答 解:(1)當m=3,n=1時,$f(x)=-\frac{1}{3}{x}^{3}-\frac{1}{2}{x}^{2}+6x$,
f′(x)=-x2-x+6=-(x-2)(x+3),
當x∈(-∞,-3)∪(2,+∞)時,f′(x)<0,當x∈(-3,2)時,f′(x)>0.
∴f(x)的單調減區間為(-∞,-3),(2,+∞);單調增區間為(-3,2).
∴f(x)的極大值為f(2)=$\frac{22}{3}$;極小值為f(-3)=$-\frac{27}{2}$.
(2)當n=-1,-2<m<0時,$f(x)=\frac{1}{3}{x}^{3}-\frac{1}{2}{x}^{2}+2mx$,f′(x)=x2-x+2m.
令f′(x)=0,得${x}_{1}=\frac{1-\sqrt{1-8m}}{2},{x}_{2}=\frac{1+\sqrt{1-8m}}{2}$,
f(x)在(-∞,x1),(x2,+∞)上單調遞增,在(x1,x2)上單調遞減.
當-2<m<0時,有x1<1<x2<4,
∴f(x)在[1,4]上的最小值為f(x2),又f(4)>f(1),
∴f(x)在[1,4]上的最大值為f(4)=8m+$\frac{40}{3}=\frac{16}{3}$.
解得m=-1,x2=2,
故f(x)在[1,4]上的最小值為f(2)=$-\frac{10}{3}$.
點評 本題考查利用導數研究函數的單調性,考查了利用導數求函數在閉區間上的最值,考查數學轉化思想方法,屬中檔題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
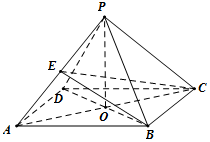 在四棱錐P-ABCD中,底面是邊長為2的菱形,∠BAD=60°,PB=PD=2,AC∩BD=O.
在四棱錐P-ABCD中,底面是邊長為2的菱形,∠BAD=60°,PB=PD=2,AC∩BD=O.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
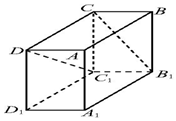 在長方體ABCD-A1B1C1D1中,B1C和C1D與底面所成的角分別為60°和45°,則異面直線B1C和C1D所成角的余弦值為( )
在長方體ABCD-A1B1C1D1中,B1C和C1D與底面所成的角分別為60°和45°,則異面直線B1C和C1D所成角的余弦值為( )| A. | $\frac{{\sqrt{6}}}{4}$ | B. | $\frac{{\sqrt{6}}}{3}$ | C. | $\frac{{\sqrt{2}}}{6}$ | D. | $\frac{{\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -3 | B. | -5 | C. | -8 | D. | 8 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
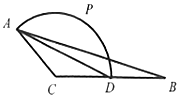 已知△ABC中,AC=2,BC=4,AB=2$\sqrt{7}$,且D是BC的中點.
已知△ABC中,AC=2,BC=4,AB=2$\sqrt{7}$,且D是BC的中點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com