
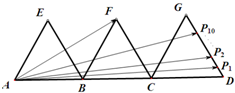
 如圖,三個邊長為2的等邊三角形有一條邊在同一條直線上,邊GD上有10個不同的點P1,P2,P3…P10,則$\overrightarrow{AF}$•($\overrightarrow{A{P_1}$+$\overrightarrow{A{P_2}}$+$\overrightarrow{A{P_3}}$+…+$\overrightarrow{A{P_{10}}}$)=180.
如圖,三個邊長為2的等邊三角形有一條邊在同一條直線上,邊GD上有10個不同的點P1,P2,P3…P10,則$\overrightarrow{AF}$•($\overrightarrow{A{P_1}$+$\overrightarrow{A{P_2}}$+$\overrightarrow{A{P_3}}$+…+$\overrightarrow{A{P_{10}}}$)=180. 分析 可用特殊位置法處理此題,假定這10個點是DG的等分點,且M為DG中點,則$\overrightarrow{A{P_1}$+$\overrightarrow{A{P_2}}$+$\overrightarrow{A{P_3}}$+…+$\overrightarrow{A{P_{10}}}$=10$\overrightarrow{AM}$,建立坐標系,向量坐標法處理數量積.
或是根據分析圖形所反應出來的幾何性質解題.
解答 解法一:特殊位置法.
令這10個點是DG的等分點,且M為DG中點,
則$\overrightarrow{A{P_1}$+$\overrightarrow{A{P_2}}$+$\overrightarrow{A{P_3}}$+…+$\overrightarrow{A{P_{10}}}$=10$\overrightarrow{AM}$,
以A為原點,AD方向為x軸建立坐標系,
故F(3,$\sqrt{3}$),M($\frac{11}{2},\frac{\sqrt{3}}{2}$)
$\overrightarrow{AF}=(3,\sqrt{3})$,$\overrightarrow{AM}=(\frac{11}{2},\frac{\sqrt{3}}{2})$
∴原式=$10\overrightarrow{AF}•\overrightarrow{AM}$=180
故答案為:180.
解法二:(幾何法)
由圖知,△AFC中,∠ACF=60°,AC=2FC=$2\sqrt{3}$,
知,△AFC為以∠AFC=90°的直角三角形.
∴AF⊥FC,∠FAC=30°.
又∵GD∥FC,∴AF⊥GD.
又 點P1,P2,…P10在線段GD上,
∴AF⊥DPi(i=1,2,3,…,10)
∴原式=$\overrightarrow{AF}•(\overrightarrow{AD}+\overrightarrow{D{P}_{1}}+$…+$\overrightarrow{AD}+\overrightarrow{D{P}_{10}})$
=$\overrightarrow{AF}•(10\overrightarrow{AD}+\overrightarrow{D{P}_{1}}+\overrightarrow{D{P}_{2}}+$…$+\overrightarrow{D{P}_{10}})$
=$10\overrightarrow{AF}•\overrightarrow{AD}+$$\overrightarrow{AF}•\overrightarrow{D{P}_{1}}$+…+$\overrightarrow{AF}•\overrightarrow{D{P}_{10}}$
=$10\overrightarrow{AF}•\overrightarrow{AD}$
=$10×2\sqrt{3}×6×cos30°$
=180.
故答案為:180.
點評 考查向量在圖形中的幾何應用,向量的加法法則,數量積的運算律,數量積的求值.分析到 AF⊥GD是解決問題的關鍵.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
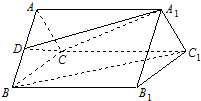 如圖,在正三棱柱ABC-A1B1C1中,點D是棱AB的中點,BC=1,AA1=$\sqrt{3}$.
如圖,在正三棱柱ABC-A1B1C1中,點D是棱AB的中點,BC=1,AA1=$\sqrt{3}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
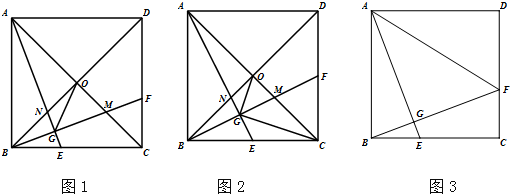
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
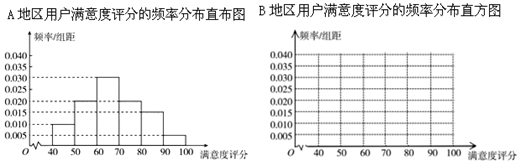
| 滿意度 評分分組 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 頻數 | 2 | 8 | 14 | 10 | 6 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $(-∞,-\frac{1}{4})∪[{2,+∞})$ | B. | $[{-\frac{1}{4},2})$ | C. | $[{-2,-\frac{1}{4}})$ | D. | $({-2,-\frac{1}{4}}]$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com