
分析 (1)消去參數(shù)t即可得到普通方程;利用sin2α+cos2α=1即可得出其參數(shù)方程C2;
(2)設(shè)$P(\sqrt{3}cosα,sinα)(α∈[0,2π))$,根據(jù)點到直線的距離公式確定d,從而得到點P的坐標(biāo).
解答 解:(1)由${C_1}:\left\{{\begin{array}{l}{x=t}\\{y=t+5}\end{array}}\right.(t$為參數(shù))消去參數(shù)t,得
C1:x-y+5=0,
曲線C2的普通方程是$\frac{{x}^{2}}{3}$+y2=1,則
${C_2}:\left\{{\begin{array}{l}{x=\sqrt{3}cosα}\\{y=sinα}\end{array}}\right.(α$為參數(shù));
(2)設(shè)$P(\sqrt{3}cosα,sinα)(α∈[0,2π))$,點P到直線x-y+5=0的距離$d=\frac{{|{\sqrt{3}cosα-sinα+5}|}}{{\sqrt{2}}}=\frac{{|{2cos(α+\frac{π}{6})+5}|}}{{\sqrt{2}}}≥\frac{3}{{\sqrt{2}}}=\frac{{3\sqrt{2}}}{2}$,
當(dāng)$cos(α+\frac{π}{6})=-1,α=\frac{5π}{6}$時,即$P(-\frac{3}{2},\frac{1}{2})$時,最短距離為$\frac{{3\sqrt{2}}}{2}$.
點評 本題考查了參數(shù)方程化為普通方程、極坐標(biāo)方程化為直角坐標(biāo)方程、點到直線的距離公式,考查了推理能力與計算能力,屬于中檔題.


 優(yōu)加精卷系列答案
優(yōu)加精卷系列答案科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 254 | B. | 255 | C. | 256 | D. | 512 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $({1,\frac{π}{4}})$ | B. | $({\sqrt{2},\frac{π}{4}})$ | C. | $({\sqrt{2},\frac{3π}{4}})$ | D. | $({\sqrt{2},-\frac{π}{4}})$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
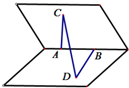 如圖,二面角α-AB-β的大小為600,棱上有A、B兩點,直線AC、BD分別在這個二面角的兩個半平面內(nèi),且都垂直于AB,已知AB=4,AC=6,BD=8,則直線AB與CD所成角的余弦值為( )
如圖,二面角α-AB-β的大小為600,棱上有A、B兩點,直線AC、BD分別在這個二面角的兩個半平面內(nèi),且都垂直于AB,已知AB=4,AC=6,BD=8,則直線AB與CD所成角的余弦值為( )| A. | $\frac{{2\sqrt{17}}}{17}$ | B. | $\frac{{\sqrt{17}}}{17}$ | C. | $\frac{{\sqrt{221}}}{17}$ | D. | $\frac{{4\sqrt{17}}}{17}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com