
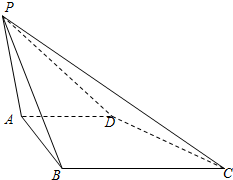
 如圖,在四棱錐P-ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,側(cè)面PAD同時垂直側(cè)面PAB與側(cè)面PDC.若PA=AB=AD=$\frac{{\sqrt{3}}}{3}$PB,則$\frac{BC}{AD}$=$\frac{3}{2}$,直線PC與底面ABCD所成角的正切值為$\frac{\sqrt{6}}{6}$.
如圖,在四棱錐P-ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,側(cè)面PAD同時垂直側(cè)面PAB與側(cè)面PDC.若PA=AB=AD=$\frac{{\sqrt{3}}}{3}$PB,則$\frac{BC}{AD}$=$\frac{3}{2}$,直線PC與底面ABCD所成角的正切值為$\frac{\sqrt{6}}{6}$. 分析 延長BA,CD交于H,連接PH,運(yùn)用面面垂直的性質(zhì)定理,可得PH⊥平面PAD,設(shè)PB=$\sqrt{3}$,可得PA=AB=AD=1,運(yùn)用余弦定理可得∠PAB,在直角三角形HPA中,∠HAP=60°,求得AH,由三角形相似知識,可得$\frac{BC}{AD}$;
求出HP,HD,PD,PC,證得AD⊥PA,又AD⊥AB,AB∩PA=A,即有AD⊥平面PAB,可得BC⊥平面PAB,設(shè)P到平面ABCD的距離為d,由VP-ABC=VC-PAB,運(yùn)用三棱錐的體積公式,求得d,運(yùn)用同角三角函數(shù)的關(guān)系,可得直線PC與底面ABCD所成角的正切值.
解答 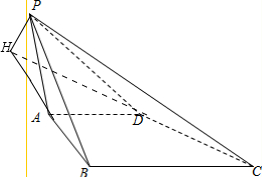 解:延長BA,CD交于H,連接PH,
解:延長BA,CD交于H,連接PH,
可得平面PAB∩平面PCD=PH,
由側(cè)面PAD同時垂直側(cè)面PAB與側(cè)面PDC,
運(yùn)用面面垂直的性質(zhì)定理,可得PH⊥平面PAD,
即有HP⊥PA,
設(shè)PB=$\sqrt{3}$,
由PA=AB=AD=$\frac{{\sqrt{3}}}{3}$PB,可得PA=AB=AD=1,
在△PAB中,由余弦定理可得,cos∠PAB=$\frac{1+1-3}{2×1×1}$=-$\frac{1}{2}$,
即有∠PAB=120°,
在直角三角形HPA中,∠HAP=60°,
可得AH=$\frac{AP}{cos∠HAP}$=$\frac{1}{cos60°}$=2,
在三角形HBC中,由三角形的相似知識可得,$\frac{BC}{AD}$=$\frac{HB}{HA}$=$\frac{3}{2}$;
在△HPA中,HP=APtan60°=$\sqrt{3}$,
在直角三角形AHD中,HD=$\sqrt{A{H}^{2}+A{D}^{2}}$=$\sqrt{4+1}$=$\sqrt{5}$,
在直角三角形HPD中,PD=$\sqrt{H{D}^{2}-H{P}^{2}}$=$\sqrt{5-3}$=$\sqrt{2}$,
PA2+AD2=PD2,可得AD⊥PA,
又AD⊥AB,AB∩PA=A,
即有AD⊥平面PAB,
由BC∥AD,可得BC⊥平面PAB,
設(shè)P到平面ABCD的距離為d,
由VP-ABC=VC-PAB,可得$\frac{1}{3}$d•S△ABC=$\frac{1}{3}$BC•S△PAB,
即$\frac{1}{3}$d•$\frac{1}{2}$•1•$\frac{3}{2}$=$\frac{1}{3}$•$\frac{3}{2}$•$\frac{1}{2}$•1•1•sin120°,
解得d=$\frac{\sqrt{3}}{2}$,
在直角三角形BCP中,PC=$\sqrt{B{C}^{2}+P{B}^{2}}$=$\sqrt{\frac{9}{4}+3}$=$\frac{\sqrt{21}}{2}$,
可得PC和平面ABCD所成角的正弦值為$\fracp9vv5xb5{PC}$=$\frac{1}{\sqrt{7}}$,
余弦值為$\sqrt{1-\frac{1}{7}}$=$\frac{\sqrt{6}}{\sqrt{7}}$,
則直線PC與底面ABCD所成角的正切值為$\frac{1}{\sqrt{6}}$=$\frac{\sqrt{6}}{6}$.
故答案為:$\frac{3}{2}$,$\frac{\sqrt{6}}{6}$.
點(diǎn)評 本題考查面面垂直的性質(zhì)定理的運(yùn)用,直線和平面所成角的正切值,考查運(yùn)算能力,運(yùn)用三角形相似知識和等積法是解題的關(guān)鍵,屬于難題.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 向左平移3個單位 | B. | 向右平移3個單位 | C. | 向左平移1個單位 | D. | 向右平移1個單位 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 80m | B. | 20m | C. | 40m | D. | 50m |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com