
分析 (1)記甲、乙、丙三人各自獨立地進行一次投籃測試投中的事件依次為A、B、C,由題設條件有:$P(A\overline{B})$=$\frac{1}{4}$,$P(B\overline{C})$=$\frac{1}{12}$,P(AC)=$\frac{2}{9}$,解出即可得出.
(2)丙連續投籃5次,恰有2次投中的概率為$P=C_5^2{(\frac{2}{3})^2}{(\frac{1}{3})^3}=\frac{40}{243}$,
(3)ξ可以取的值為0,2,4,5,9,可求得:$P(ξ=0)={(\frac{1}{3})^3}=\frac{1}{27}$,$P(ξ=2)=C_3^1\frac{2}{3}{(\frac{1}{3})^2}=\frac{2}{9}$,$P(ξ=4)={(\frac{2}{3})^2}\frac{1}{3}=\frac{4}{27}$,$P(ξ=5)=2{(\frac{2}{3})^2}\frac{1}{3}=\frac{8}{27}$,$P(ξ=9)={(\frac{2}{3})^3}=\frac{8}{27}$.可得ξ的分布列及其數學期望.
解答 解:(1)記甲、乙、丙三人各自獨立地進行一次投籃測試投中的事件依次為A、B、C,由題設條件有:
$P(A\overline{B})$=$\frac{1}{4}$,$P(B\overline{C})$=$\frac{1}{12}$,P(AC)=$\frac{2}{9}$,即P(A)[1-P(B)]=$\frac{1}{4}$,①;P(B)[1-P(C)]=$\frac{1}{12}$,②P(A)P(C)=$\frac{2}{9}$,③.…(2分)
由①③得P(B)=1-$\frac{9}{8}$P(C),代入②得27P(C)]2-51P(C)+22=0.
解得P(C)=$\frac{2}{3}$或P(C)=$\frac{11}{9}$ (舍去).將P(C)=$\frac{2}{3}$分別代入②③可得P(A)=$\frac{1}{3}$,P(B)=$\frac{1}{4}$.
故甲、乙、丙三人各自投籃一次投中的概率分別是$\frac{1}{3}$,$\frac{1}{4}$,$\frac{2}{3}$…(5分)
(2)丙連續投籃5次,恰有2次投中的概率為$P=C_5^2{(\frac{2}{3})^2}{(\frac{1}{3})^3}=\frac{40}{243}$;…(7分)
(3)ξ可以取的值為0,2,4,5,9,可求得:$P(ξ=0)={(\frac{1}{3})^3}=\frac{1}{27}$,$P(ξ=2)=C_3^1\frac{2}{3}{(\frac{1}{3})^2}=\frac{2}{9}$,$P(ξ=4)={(\frac{2}{3})^2}\frac{1}{3}=\frac{4}{27}$,$P(ξ=5)=2{(\frac{2}{3})^2}\frac{1}{3}=\frac{8}{27}$,$P(ξ=9)={(\frac{2}{3})^3}=\frac{8}{27}$.
∴ξ的分布列為:
| ξ | 0 | 2 | 4 | 5 | 9 |
| p | $\frac{1}{27}$ | $\frac{2}{9}$ | $\frac{4}{27}$ | $\frac{8}{27}$ | $\frac{8}{27}$ |
點評 本題考查了相互獨立、互斥事件的概率計算公式及其數學期望,考查推理能力與計算能力,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
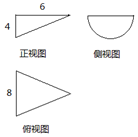 某幾何體的三視圖是如圖所示的直角三角形、半圓和等腰三角形,各邊的長度如圖所示,則此幾何體的體積是16π,表面積是$24+(8+4\sqrt{13})π$.
某幾何體的三視圖是如圖所示的直角三角形、半圓和等腰三角形,各邊的長度如圖所示,則此幾何體的體積是16π,表面積是$24+(8+4\sqrt{13})π$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,在四棱錐中P-ABCD,AB=BC=CD=DA,∠BAD=60°,AQ=QD,△PAD是正三角形.
如圖,在四棱錐中P-ABCD,AB=BC=CD=DA,∠BAD=60°,AQ=QD,△PAD是正三角形.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com