
【題目】已知函數![]() ,
,![]() ,
,![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 的極值;
的極值;
(2)若在區間![]() 上存在不相等的實數
上存在不相等的實數![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范圍;
的取值范圍;
(3)設![]() 的圖象為
的圖象為![]() ,
,![]() 的圖象為
的圖象為![]() ,若直線
,若直線![]() 與
與![]() 分別交于
分別交于![]() ,問是否存在整數
,問是否存在整數![]() ,使
,使![]() 在
在![]() 處的切線與
處的切線與![]() 在
在![]() 處的切線互相平行,若存在,求出
處的切線互相平行,若存在,求出![]() 的所有值,若不存在,請說明理由.
的所有值,若不存在,請說明理由.
【答案】(1)極大值為![]() ,無極小值;(2)
,無極小值;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)對函數![]() 進行求導,并求出方程
進行求導,并求出方程![]() 的根為
的根為![]() ,判斷
,判斷![]() 為函數的極大值點,再代入求極大值;
為函數的極大值點,再代入求極大值;
(2)問題轉化成函數![]() 在區間
在區間![]() 存在極值點;
存在極值點;
(3)根據兩條切線互相平行,得到斜率相等,從而構造出![]() 的方程,再從方程中把
的方程,再從方程中把![]() 分離出來,構造關于
分離出來,構造關于![]() 的函數,研究函數的值域,得到
的函數,研究函數的值域,得到![]() 的取值范圍后,再根據
的取值范圍后,再根據![]() 為整數,求得
為整數,求得![]() 的值.
的值.
(1)當![]() 時,
時,![]() ,
,![]() ,
,
當![]() 時,得
時,得![]() ,當
,當![]() 時,得
時,得![]() ,
,
所以![]() 在
在![]() 單調遞增,在
單調遞增,在![]() 單調遞減,
單調遞減,
所以![]() ,無極小值.
,無極小值.
(2)令![]() ,則
,則
![]() ,
,
由題意知![]() 在區間
在區間![]() 存在極值點,所以
存在極值點,所以![]() 在
在![]() 有解,
有解,
所以![]()
![]() 在
在![]() 有解,
有解,
令![]() ,則
,則![]() ,
,
當![]() 時,
時,![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 單調遞增,且
單調遞增,且![]()
![]() ,
,
所以![]() .
.
(3)![]()
![]()
![]() ,則
,則![]()
![]() ,
,
![]()
![]() ,則
,則![]() ,
,
設![]() ,
,![]() ,
,
在點![]() 處的切線的斜率
處的切線的斜率![]() ,在點
,在點![]() 處的切線的斜率
處的切線的斜率![]() ,
,
假設存在兩切線平行,所以![]() ,即
,即![]()
![]() 在
在![]() 有解,
有解,
所以![]() 在
在![]() 有解,令
有解,令![]() ,則
,則![]() ,
,![]() ,
,
當![]() 時,得
時,得![]() ;當
;當![]() 時,得
時,得![]() ,
,
所以![]() 在
在![]() 單調遞增,在
單調遞增,在![]() 單調遞減,
單調遞減,
所以![]()
![]() ,
,
所以![]() 在
在![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 單調遞減,
單調遞減,
所以![]() ,則
,則![]() ,又
,又![]() 為整數,
為整數,
所以![]() 或
或![]() .
.


 作業輔導系列答案
作業輔導系列答案 同步學典一課多練系列答案
同步學典一課多練系列答案 經典密卷系列答案
經典密卷系列答案 金牌課堂練系列答案
金牌課堂練系列答案科目:高中數學 來源: 題型:
【題目】已知P(![]() ,1),Q(cosx,sinx),O為坐標原點,函數f(x)
,1),Q(cosx,sinx),O為坐標原點,函數f(x)![]() .
.
(1)求f(x)的解析式及最小正周期;
(2)若A為△ABC的內角,f(A)=4,BC=3,△ABC的面積為![]() ,求AB+AC.
,求AB+AC.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 年以來精準扶貧政策的落實,使我國扶貧工作有了新進展,貧困發生率由
年以來精準扶貧政策的落實,使我國扶貧工作有了新進展,貧困發生率由![]() 年底的
年底的![]() 下降到
下降到![]() 年底的
年底的![]() ,創造了人類減貧史上的的中國奇跡.“貧困發生率”是指低于貧困線的人口占全體人口的比例,
,創造了人類減貧史上的的中國奇跡.“貧困發生率”是指低于貧困線的人口占全體人口的比例,![]() 年至
年至![]() 年我國貧困發生率的數據如下表:
年我國貧困發生率的數據如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
貧困發生率 | 10.2 | 8.5 | 7.2 | 5.7 | 4.5 | 3.1 | 1.4 |
(1)從表中所給的![]() 個貧困發生率數據中任選兩個,求兩個都低于
個貧困發生率數據中任選兩個,求兩個都低于![]() 的概率;
的概率;
(2)設年份代碼![]() ,利用線性回歸方程,分析
,利用線性回歸方程,分析![]() 年至
年至![]() 年貧困發生率
年貧困發生率![]() 與年份代碼
與年份代碼![]() 的相關情況,并預測
的相關情況,并預測![]() 年貧困發生率.
年貧困發生率.
附:回歸直線![]() 的斜率和截距的最小二乘估計公式分別為:
的斜率和截距的最小二乘估計公式分別為:
 (
(![]() 的值保留到小數點后三位)
的值保留到小數點后三位)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,底面ABCD是菱形,PA=PD,∠DAB=60°.
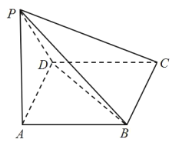
(1)證明:AD⊥PB.
(2)若PB=![]() ,AB=PA=2,求三棱錐P-BCD的體積。
,AB=PA=2,求三棱錐P-BCD的體積。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某人承攬一項業務,需做文字標牌4個,繪畫標牌5個,現有兩種規格的原料,甲種規格每張3m2,可做文字標牌1個,繪畫標牌2個,乙種規格每張2m2,可做文字標牌2個,繪畫標牌1個,求兩種規格的原料各用多少張,才能使總的用料面積最小?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某調研機構,對本地![]() 歲的人群隨機抽取
歲的人群隨機抽取![]() 人進行了一次生活習慣是否符合低碳觀念的調查,將生活習慣符合低碳觀念的稱為“低碳族”,否則稱為“非低碳族”,結果顯示,有
人進行了一次生活習慣是否符合低碳觀念的調查,將生活習慣符合低碳觀念的稱為“低碳族”,否則稱為“非低碳族”,結果顯示,有![]() 人為“低碳族”,該
人為“低碳族”,該![]() 人的年齡情況對應的頻率分布直方圖如圖.
人的年齡情況對應的頻率分布直方圖如圖.
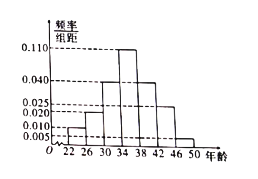
(1)根據頻率分布直方圖,估計這![]() 名“低碳族”年齡的平均值,中位數;
名“低碳族”年齡的平均值,中位數;
(2)若在“低碳族”且年齡在![]() 、
、![]() 的兩組人群中,用分層抽樣的方法抽取
的兩組人群中,用分層抽樣的方法抽取![]() 人,試估算每個年齡段應各抽取多少人?
人,試估算每個年齡段應各抽取多少人?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com