
【題目】某人承攬一項業務,需做文字標牌4個,繪畫標牌5個,現有兩種規格的原料,甲種規格每張3m2,可做文字標牌1個,繪畫標牌2個,乙種規格每張2m2,可做文字標牌2個,繪畫標牌1個,求兩種規格的原料各用多少張,才能使總的用料面積最小?

【答案】使用甲種規格原料2張,乙種規格原料1張,可使總的用料面積最小.
【解析】
本題考查的知識點是簡單的線性規劃的應用,根據已知條件中解:需要甲種原料x張,乙種原料y張,則可做文字標牌(x+2y)個,繪畫標牌(2x+y)個,由題意得出約束條件,及目標函數,然后利用線性規劃,求出最優解.
解:設需要甲種原料x張,乙種原料y張,
則可做文字標牌(x+2y)個,繪畫標牌(2x+y)個.
由題意可得:
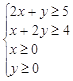
所用原料的總面積為z=3x+2y,作出可行域如圖,
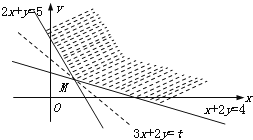
在一組平行直線3x+2y=t中,經過可行域內的點且到原點距離最近的直線
過直線2x+y=5和直線x+2y=4的交點(2,1),∴最優解為:x=2,y=1
∴使用甲種規格原料2張,乙種規格原料1張,可使總的用料面積最小.


科目:高中數學 來源: 題型:
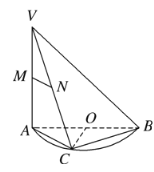
【題目】如圖所示,![]() 是半圓
是半圓![]() 的直徑,
的直徑,![]() 垂直于半圓
垂直于半圓![]() 所在的平面,點
所在的平面,點![]() 是圓周上不同于
是圓周上不同于![]() 的任意一點,
的任意一點,![]() 分別為
分別為![]() 的中點,則下列結論正確的是( )
的中點,則下列結論正確的是( )
A.![]() B.平面
B.平面![]() 平面
平面![]()
C.![]() 與
與![]() 所成的角為45°D.
所成的角為45°D.![]() 平面
平面![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】△ABC的內角A,B,C的對邊分別為a,b,c,已知sin(A+C)=8sin2 ![]() .
.
(Ⅰ)求cosB;
(Ⅱ)若a+c=6,△ABC面積為2,求b.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種零件按質量標準分為1,2,3,4,5五個等級.現從一批該零件中隨機抽取20個,對其等級進行統計分析,得到頻率分布表如下:

(1)在抽取的20個零件中,等級為5的恰有2個,求![]() ;
;
(2)在(1)的條件下,從等級為3和5的所有零件中,任意抽取2個,求抽取的2個零件等級恰好相同的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數exf(x)(e≈2.71828…是自然對數的底數)在f(x)的定義域上單調遞增,則稱函數f(x)具有M性質.下列函數中所有具有M性質的函數的序號為 .
①f(x)=2﹣x②f(x)=3﹣x③f(x)=x3④f(x)=x2+2.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com