
【題目】若函數exf(x)(e≈2.71828…是自然對數的底數)在f(x)的定義域上單調遞增,則稱函數f(x)具有M性質.下列函數中所有具有M性質的函數的序號為 .
①f(x)=2﹣x②f(x)=3﹣x③f(x)=x3④f(x)=x2+2.
【答案】①④
【解析】解:對于①,f(x)=2﹣x , 則g(x)=exf(x)= ![]() 為實數集上的增函數;
為實數集上的增函數;
對于②,f(x)=3﹣x , 則g(x)=exf(x)= ![]() 為實數集上的減函數;
為實數集上的減函數;
對于③,f(x)=x3 , 則g(x)=exf(x)=exx3 ,
g′(x)=exx3+3exx2=ex(x3+3x2)=exx2(x+3),當x<﹣3時,g′(x)<0,
∴g(x)=exf(x)在定義域R上先減后增;
對于④,f(x)=x2+2,則g(x)=exf(x)=ex(x2+2),
g′(x)=ex(x2+2)+2xex=ex(x2+2x+2)>0在實數集R上恒成立,
∴g(x)=exf(x)在定義域R上是增函數.
∴具有M性質的函數的序號為①④.
所以答案是:①④.
【考點精析】根據題目的已知條件,利用函數單調性的性質和指數函數的圖像與性質的相關知識可以得到問題的答案,需要掌握函數的單調區間只能是其定義域的子區間 ,不能把單調性相同的區間和在一起寫成其并集;a0=1, 即x=0時,y=1,圖象都經過(0,1)點;ax=a,即x=1時,y等于底數a;在0<a<1時:x<0時,ax>1,x>0時,0<ax<1;在a>1時:x<0時,0<ax<1,x>0時,ax>1.


科目:高中數學 來源: 題型:
【題目】某人承攬一項業務,需做文字標牌4個,繪畫標牌5個,現有兩種規格的原料,甲種規格每張3m2,可做文字標牌1個,繪畫標牌2個,乙種規格每張2m2,可做文字標牌2個,繪畫標牌1個,求兩種規格的原料各用多少張,才能使總的用料面積最小?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩名同學參加一項射擊比賽游戲,其中任何一人每射擊一次擊中目標得2分,未擊中目標得0分.若甲、乙兩人射擊的命中率分別為 ![]() 和P,且甲、乙兩人各射擊一次得分之和為2的概率為
和P,且甲、乙兩人各射擊一次得分之和為2的概率為 ![]() .假設甲、乙兩人射擊互不影響,則P值為( )
.假設甲、乙兩人射擊互不影響,則P值為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在如圖所示的十一面體![]() 中,用
中,用![]() 種不同顏色給這個幾何體各個頂點染色,每個頂點染一種顏色,要求每條棱的兩端點異色,則不同的染色方案種數為__________.
種不同顏色給這個幾何體各個頂點染色,每個頂點染一種顏色,要求每條棱的兩端點異色,則不同的染色方案種數為__________.
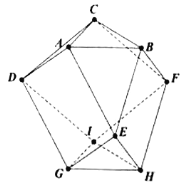
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)是定義在(﹣∞,0)上的可導函數,其導函數為f′(x),且有xf′(x)>x2+3f(x),則不等式8f(x+2014)+(x+2014)3f(﹣2)>0的解集為( )
A.(﹣∞,﹣2016)
B.(﹣2018,﹣2016)
C.(﹣2018,0)
D.(﹣∞,﹣2018)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設關于 x 的函數f(x)=lg(x2﹣2x﹣3)的定義域為集合 A,函數 g(x)=x﹣a,(0≤x≤4)的值域為集合 B.
(1)求集合 A,B;
(2)若集合 A,B 滿足 A∩B=B,求實數 a 的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com