Question

10．如圖，在四棱錐P-ABCD中，AB⊥平面BCP，CD∥平面ABP，AB=BC=CP=BP=2CD=2
（1）證明：平面ABP⊥平面ADP；
（2）若直線PA與平面PCD所成角為α，求sinα的值．

Answer 1

分析 （1）取AP的中點E，PB的中點F，連結DE，EF，CF，利用平行四邊形得出DE∥CF，通過證明CF⊥平面APB得出DE⊥平面PAB，于是平面ABP⊥平面ADP；
（2）將幾何體補成直三棱柱，作出線面角，從而可求出sinα的值．

解答 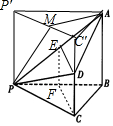（1）證明：取AP的中點E，PB的中點F，連結DE，EF，CF，
則EF$\stackrel{∥}{=}$$\frac{1}{2}$AB，
∵CD∥平面ABP，CD?平面ABCD，平面ABCD∩平面ABP=AB，
∴CD∥AB，又CD=$\frac{1}{2}$AB，
∴EF$\stackrel{∥}{=}$CD，
∴四邊形DEFC是平行四邊形，∴CF∥DE，
∵AB⊥平面BCP，CF?平面BCP，
∴AB⊥CF，
∵BC=CP=BP，
∴CF⊥PB，又PB∩AB=B，
∴CF⊥平面ABP，
∴DE⊥平面ABP，又DE?平面ADP，
∴平面ABP⊥平面ADP．
（2）解：過P作PP′∥AB，使得PP′=2，延長CD到C′，使得CC′=2，連結AC′，AP′，C′P′，
則直三棱柱PBC-P′AC′所有棱長均為2，
取P′C′的中點M，連結AM，則AM⊥平面PCC′P′，
∴∠APM是直線AP與平面PCD所成的角，即∠APM=α，
∵AM=$\sqrt{AP{′}^{2}-P′{M}^{2}}$=$\sqrt{3}$，PA=$\sqrt{P{B}^{2}+A{B}^{2}}$=2$\sqrt{2}$，
∴sinα=sin∠APM=$\frac{AM}{AP}$=$\frac{\sqrt{3}}{2\sqrt{2}}$=$\frac{\sqrt{6}}{4}$．

點評 本題考查了面面垂直的判定，直線與平面所成角的計算，屬于中檔題．