Question

17．已知雙曲線$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦點為F，若過F且傾斜角為60°的直線分別與雙曲線的左右兩支相交，則此雙曲線離心率的取值范圍是（2，+∞）．

Answer 1

分析 根據已知直線的斜率，求出漸近線的斜率范圍，推出a，b的關系，然后求出離心率的范圍．

解答 解：依題意，斜率為$\sqrt{3}$的直線l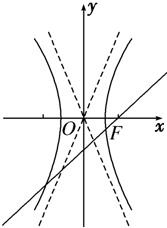過雙曲線$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）
的右焦點為F且與雙曲線的左右兩支分別相交，
結合圖形分析可知，
雙曲線的一條漸近線的斜率$\frac{b}{a}$必大于$\sqrt{3}$，
即$\frac{b}{a}$＞$\sqrt{3}$，
因此該雙曲線的離心率e=$\frac{c}{a}$=$\sqrt{1+（\frac{b}{a}）^{2}}$＞$\sqrt{1+3}$=2．
故答案為：（2，+∞）．

點評 本題考查直線的斜率，雙曲線的應用，考查轉化思想，是基礎題．