
【題目】已知數列![]() ,若對任意
,若對任意![]() ,都有
,都有![]() 成立,則稱數列
成立,則稱數列![]() 為“差增數列”.
為“差增數列”.
(1)試判斷數列![]() 是否為“差增數列”,并說明理由;
是否為“差增數列”,并說明理由;
(2)若數列![]() 為“差增數列”,且
為“差增數列”,且![]() ,
,![]() ,對于給定的正整數m,當
,對于給定的正整數m,當![]() ,項數k的最大值為20時,求m的所有可能取值的集合;
,項數k的最大值為20時,求m的所有可能取值的集合;
(3)若數列![]() 為“差增數列”,
為“差增數列”,![]() ,且
,且![]() ,證明:
,證明:![]() .
.
【答案】(1)是;見解析(2)![]() ;(3)見解析
;(3)見解析
【解析】
(1)數列![]() 是“差增數列”.由新定義可知,只要證明
是“差增數列”.由新定義可知,只要證明![]() >an+1即可;
>an+1即可;
(2)由新定義可得對任意的n∈N*,an+2﹣an+1>an+1﹣an恒成立,可令bn=an+1﹣an(n≥1),運用累加法,結合等差數列的求和公式可得an,由于1≤n≤19,結合條件可得m的取值集合;
(3)運用反證法證明,假設x1010x1011≥1,由題意可得x1x2…x2020=1,![]() <
<![]() ,運用不等式的性質推得x1009x1012>1,即可得到矛盾,進而得證.
,運用不等式的性質推得x1009x1012>1,即可得到矛盾,進而得證.
解:(1)數列![]() 是“差增數列”.
是“差增數列”.
因為任意的n∈N*,都有an+an+2=n2+(n+2)2=2n2+4n+4=2(n+1)2+2>2(n+1)2=2an+1,
即![]() >an+1成立,
>an+1成立,
所以數列![]() 是“差增數列”;
是“差增數列”;
(2)由已知,對任意的n∈N*,an+2﹣an+1>an+1﹣an恒成立.
可令bn=an+1﹣an(n≥1),則bn∈N,且bn<bn+1,
又an=m,要使項數k達到最大,且最大值為20時,必須bn(1≤n≤18)最小.
而b1=0,故b2=1,b3=2,…,bn=n﹣1.
所以an﹣a1=b1+b2+…+bn﹣1=0+1+2+…+(n﹣2)=![]() (n﹣1)(n﹣2),
(n﹣1)(n﹣2),
即當1≤n≤19時,an=1+![]() ,a19=154,因為k的最大值為20,
,a19=154,因為k的最大值為20,
所以18≤a20﹣a19<18+19,即18≤m﹣154<18+19,
所以m的所有可能取值的集合為{m|172≤m<191,m∈N*}.
(3)證明:(反證法)假設x1010x1011≥1.由已知可得xn(n=1,2,…,2020)均為正數,且x1x2…x2020=1,![]() <
<![]() .
.
而由![]() <
<![]() 可得
可得![]() <
<![]() <
<![]() ,
,
即x1010x1011<x1009x1012,所以x1009x1012>1.
又![]() =
=![]()
![]() <
<![]()
![]() =
=![]() ,即x1008x1013>1,
,即x1008x1013>1,
同理可證x1007x1014>1,…,x1x2020>1,
因此x1x2…x2020>1,這與已知矛盾,
所以x1010x1011<1.


 新思維假期作業寒假吉林大學出版社系列答案
新思維假期作業寒假吉林大學出版社系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() (
(![]() )的離心率為
)的離心率為![]() ,過右焦點且垂直于長軸的直線與橢圓C交于P,Q兩點,且
,過右焦點且垂直于長軸的直線與橢圓C交于P,Q兩點,且![]() .
.
(1)求橢圓C的方程;
(2)A,B是橢圓C上的兩個不同點,若直線![]() ,
,![]() 的斜率之積為
的斜率之積為![]() (以O為坐標原點),M是
(以O為坐標原點),M是![]() 的中點,連接
的中點,連接![]() 并延長交橢圓C于點N,求
并延長交橢圓C于點N,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() ,
,![]() ).
).
(1)當![]() 時,若函數
時,若函數![]() 在
在![]() 上有兩個零點,求
上有兩個零點,求![]() 的取值范圍;
的取值范圍;
(2)當![]() 時,是否存在
時,是否存在![]() ,使得不等式
,使得不等式![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值集合;若不存在,請說明理由.
的取值集合;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設無窮數列![]() 的前
的前![]() 項和為
項和為![]() ,已知
,已知![]() ,
,![]() .
.
(1)求![]() 的值;
的值;
(2)求數列![]() 的通項公式;
的通項公式;
(3)是否存在數列![]() 的一個無窮子數列
的一個無窮子數列![]() ,使
,使![]() 對一切
對一切![]() 均成立?若存在,請寫出數列
均成立?若存在,請寫出數列![]() 的所有通項公式;若不存在,請說明理由.
的所有通項公式;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,曲線C的參數方程為![]() ,(θ為參數),以原點為極點,x軸非負半軸為極軸建立極坐標系.
,(θ為參數),以原點為極點,x軸非負半軸為極軸建立極坐標系.
(1)求曲線C的極坐標方程;
(2)在平面直角坐標系xOy中,A(﹣2,0),B(0,﹣2),M是曲線C上任意一點,求△ABM面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區城鄉居民儲蓄存款年底余額(單位:億元)如圖所示,下列判斷一定不正確的是( )
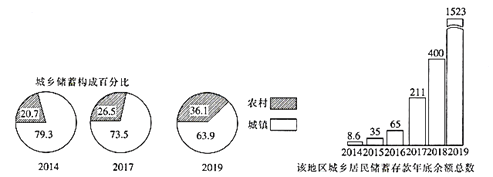
A.城鄉居民儲蓄存款年底余額逐年增長
B.農村居民的存款年底余額所占比重逐年上升
C.到2019年農村居民存款年底總余額已超過了城鎮居民存款年底總余額
D.城鎮居民存款年底余額所占的比重逐年下降
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三棱維![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 的中點,點
的中點,點![]() 在棱
在棱![]() 上點
上點![]() 是
是![]() 的重心.
的重心.
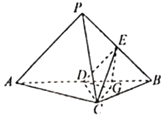
(1)若![]() 是
是![]() 的中點,證明
的中點,證明![]() 面
面![]() ;
;
(2)是否存在點![]() ,使二面角
,使二面角![]() 的大小為
的大小為![]() ,若存在,求
,若存在,求![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com