
分析 (1)每擲1個骰子都有6種情況,所以同時擲兩個骰子總的結果數為6×6=36.向上的數相同的結果有6種,由此能求出向上的數相同的概率.
(2)向上的數之積為偶數的情況比較多,可以先考慮其對立事件,即向上的數之積為奇數.利用列舉法求出向上的數之積為奇數的基本事件個數,由此利用對立事件概率計算公式能求出向上的數之積為偶數的概率.
解答 解:(1)每擲1個骰子都有6種情況,所以同時擲兩個骰子總的結果數為6×6=36.
向上的數相同的結果有6種,故向上的數相同的概率為P(A)=$\frac{6}{36}$=$\frac{1}{6}$.
(2)向上的數之積為偶數的情況比較多,可以先考慮其對立事件,即向上的數之積為奇數.
向上的數之積為奇數的基本事件有:
(1,1),(1,3),(1,5),(3,1),(3,3),(3,5),(5,1),(5,3),(5,5),共9個,
故向上的數之積為偶數的概率為P(B)=1-$\frac{9}{36}$=1-$\frac{1}{4}$=$\frac{3}{4}$.
點評 本題考查概率的求法,是基礎題,解題時要認真審題,注意列舉法的合理運用.


科目:高中數學 來源: 題型:選擇題
| A. | 1:3 | B. | 1 | C. | 5:3 | D. | 3:5 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
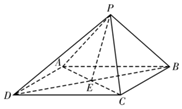 如圖,四棱錐P-ABCD的底面ABCD是菱形,∠ADC=60°,PA=PC,PD⊥PB,AC∩BD=E,二面角P-AC-B的大小為60°.
如圖,四棱錐P-ABCD的底面ABCD是菱形,∠ADC=60°,PA=PC,PD⊥PB,AC∩BD=E,二面角P-AC-B的大小為60°.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
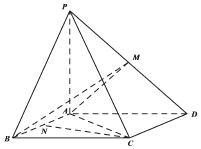 如圖,四棱錐P-ABCD中,底面ABCD為平行四邊形,PA⊥底面ABCD,M是棱PD的中點,且PA=AB=AC=2,BC=2$\sqrt{2}$.
如圖,四棱錐P-ABCD中,底面ABCD為平行四邊形,PA⊥底面ABCD,M是棱PD的中點,且PA=AB=AC=2,BC=2$\sqrt{2}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 10 | B. | 19 | C. | 20 | D. | 30 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{8}{3}$ | B. | $\frac{11}{6}$ | C. | $\frac{11}{3}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com