
【題目】設(shè)![]() 為給定的不小于
為給定的不小于![]() 的正整數(shù),考察
的正整數(shù),考察![]() 個(gè)不同的正整數(shù)
個(gè)不同的正整數(shù)![]() ,
,![]() ,
,![]() ,
,![]() 構(gòu)成的集合
構(gòu)成的集合![]() ,若集合
,若集合![]() 的任何兩個(gè)不同的非空子集所含元素的總和均不相等,則稱集合
的任何兩個(gè)不同的非空子集所含元素的總和均不相等,則稱集合![]() 為“差異集合”.
為“差異集合”.
(1)分別判斷集合![]() ,集合
,集合![]() 是否是“差異集合”;(只需寫出結(jié)論)
是否是“差異集合”;(只需寫出結(jié)論)
(2)設(shè)集合![]() 是“差異集合”,記
是“差異集合”,記![]() ,求證:數(shù)列
,求證:數(shù)列![]() 的前
的前![]() 項(xiàng)和
項(xiàng)和![]()
![]() ;
;
(3)設(shè)集合![]() 是“差異集合”,求
是“差異集合”,求![]() 的最大值.
的最大值.
 輕松奪冠全能掌控卷系列答案
輕松奪冠全能掌控卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 為定義在
為定義在![]() 上的奇函數(shù),當(dāng)
上的奇函數(shù),當(dāng)![]() 時(shí),有
時(shí),有![]() ,且當(dāng)
,且當(dāng)![]() 時(shí),
時(shí),![]() ,下列命題正確的是( )
,下列命題正確的是( )
A.![]() B.函數(shù)
B.函數(shù)![]() 在定義域上是周期為
在定義域上是周期為![]() 的函數(shù)
的函數(shù)
C.直線![]() 與函數(shù)
與函數(shù)![]() 的圖象有
的圖象有![]() 個(gè)交點(diǎn)D.函數(shù)
個(gè)交點(diǎn)D.函數(shù)![]() 的值域?yàn)?/span>
的值域?yàn)?/span>![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】近年來,共享單車已經(jīng)悄然進(jìn)入了廣大市民的日常生活,并慢慢改變了人們的出行方式.為了更好地服務(wù)民眾,某共享單車公司在其官方![]() 中設(shè)置了用戶評價(jià)反饋系統(tǒng),以了解用戶對車輛狀況和優(yōu)惠活動的評價(jià),現(xiàn)從評價(jià)系統(tǒng)中選出
中設(shè)置了用戶評價(jià)反饋系統(tǒng),以了解用戶對車輛狀況和優(yōu)惠活動的評價(jià),現(xiàn)從評價(jià)系統(tǒng)中選出![]() 條較為詳細(xì)的評價(jià)信息進(jìn)行統(tǒng)計(jì),車輛狀況和優(yōu)惠活動評價(jià)的
條較為詳細(xì)的評價(jià)信息進(jìn)行統(tǒng)計(jì),車輛狀況和優(yōu)惠活動評價(jià)的![]() 列聯(lián)表如下:
列聯(lián)表如下:
對優(yōu)惠活動好評 | 對優(yōu)惠活動不滿意 | 合計(jì) | |
對車輛狀況好評 |
|
|
|
對車輛狀況不滿意 |
|
|
|
合計(jì) |
|
|
|
(1)能否在犯錯(cuò)誤的概率不超過![]() 的前提下認(rèn)為優(yōu)惠活動好評與車輛狀況好評之間有關(guān)系?
的前提下認(rèn)為優(yōu)惠活動好評與車輛狀況好評之間有關(guān)系?
(2)為了回饋用戶,公司通過![]() 向用戶隨機(jī)派送每張的面額為
向用戶隨機(jī)派送每張的面額為![]() 元,
元,![]() 元,
元,![]() 元的三種騎行券,用戶每次使用
元的三種騎行券,用戶每次使用![]() 掃碼用車后,都可獲得一張騎行券,用戶騎行一-次獲得
掃碼用車后,都可獲得一張騎行券,用戶騎行一-次獲得![]() 元券,獲得
元券,獲得![]() 元券的概率分別是
元券的概率分別是![]() ,且各次獲取騎行券的結(jié)果相互獨(dú)立.若某用戶一天使用了兩次該公司的共享單車,記該用戶當(dāng)天獲得的騎行券面額之和為
,且各次獲取騎行券的結(jié)果相互獨(dú)立.若某用戶一天使用了兩次該公司的共享單車,記該用戶當(dāng)天獲得的騎行券面額之和為![]() ,求隨機(jī)變量
,求隨機(jī)變量![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
附:下邊的臨界值表僅供參考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(參考公式: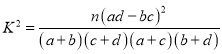 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時(shí),討論
時(shí),討論![]() 的單調(diào)性;
的單調(diào)性;
(2)設(shè)函數(shù)![]() ,若存在不相等的實(shí)數(shù)
,若存在不相等的實(shí)數(shù)![]() ,
,![]() ,使得
,使得![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列![]() 中,已知
中,已知![]() ,
,![]() 對任意
對任意![]() 都成立,數(shù)列
都成立,數(shù)列![]() 的前n項(xiàng)和為
的前n項(xiàng)和為![]() .
.
(1)若![]() 是等差數(shù)列,求k的值;
是等差數(shù)列,求k的值;
(2)若![]() ,
,![]() ,求
,求![]() ;
;
(3)是否存在實(shí)數(shù)k,使數(shù)列![]() 是公比不為1的等比數(shù)列,且任意相鄰三項(xiàng)
是公比不為1的等比數(shù)列,且任意相鄰三項(xiàng)![]() ,
,![]() ,
,![]() 按某順序排列后成等差數(shù)列?若存在,求出所有k的值;若不存在,請說明理由.
按某順序排列后成等差數(shù)列?若存在,求出所有k的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】對于雙曲線![]() ,定義
,定義![]() 為其伴隨曲線,記雙曲線
為其伴隨曲線,記雙曲線![]() 的左、右頂點(diǎn)為
的左、右頂點(diǎn)為![]() 、
、![]() .
.
(1)當(dāng)![]() 時(shí),記雙曲線
時(shí),記雙曲線![]() 的半焦距為
的半焦距為![]() ,其伴隨橢圓
,其伴隨橢圓![]() 的半焦距為
的半焦距為![]() ,若
,若![]() ,求雙曲線
,求雙曲線![]() 的漸近線方程.
的漸近線方程.
(2)若雙曲線![]() 的方程為
的方程為![]() ,弦
,弦![]() 軸,記直線
軸,記直線![]() 與直線
與直線![]() 的交點(diǎn)為
的交點(diǎn)為![]() ,求其動點(diǎn)
,求其動點(diǎn)![]() 的軌跡方程.
的軌跡方程.
(3)過雙曲線![]() 的左焦點(diǎn)
的左焦點(diǎn)![]() ,且斜率為
,且斜率為![]() 的直線
的直線![]() 與雙曲線
與雙曲線![]() 交于
交于![]() 兩點(diǎn),求證:對任意的
兩點(diǎn),求證:對任意的![]() ,在伴隨曲線
,在伴隨曲線![]() 上總存在點(diǎn)
上總存在點(diǎn)![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示的幾何體中,正方形![]() 所在平面垂直于平面
所在平面垂直于平面![]() ,四邊形
,四邊形![]() 為平行四邊形,
為平行四邊形,![]() 為
為![]() 上一點(diǎn),且
上一點(diǎn),且![]() 平面
平面![]() ,
,![]() .
.
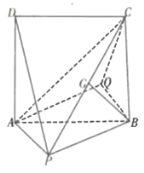
(1)求證:平面![]() 平面
平面![]() ;
;
(2)當(dāng)三棱錐![]() 體積最大時(shí),求直線
體積最大時(shí),求直線![]() 與平面
與平面![]() 所成角的正切值.
所成角的正切值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() 是兩條不同的直線,
是兩條不同的直線,![]() 是兩個(gè)不同的平面,則下列命題中正確命題的序號是( )
是兩個(gè)不同的平面,則下列命題中正確命題的序號是( )
①若直線![]() 平行于平面
平行于平面![]() 內(nèi)的無數(shù)條直線,則直線
內(nèi)的無數(shù)條直線,則直線![]() ∥平面
∥平面![]() .
.
②若直線![]() ∥平面
∥平面![]() ,直線
,直線![]() ∥直線
∥直線![]() ,則直線
,則直線![]() 平行于平面
平行于平面![]() 內(nèi)的無數(shù)條直線.
內(nèi)的無數(shù)條直線.
③若直線![]() 不平行,則
不平行,則![]() 不可能垂直于同一平面.
不可能垂直于同一平面.
④若直線![]() ∥平面
∥平面![]() ,平面
,平面![]() 平面
平面![]() ,則直線
,則直線![]() 平面
平面![]()
A.①②B.②③C.②④D.③④
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在三棱錐![]() 中,
中,![]() 為正三角形,
為正三角形,![]() 為棱
為棱![]() 的中點(diǎn),
的中點(diǎn),![]() ,
,![]() ,平面
,平面![]() 平面
平面![]()
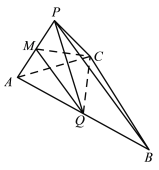
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若![]() 是棱
是棱![]() 上一點(diǎn),
上一點(diǎn),![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,求二面角
,求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com