Question

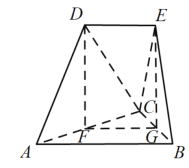
【題目】如圖所示的幾何體中，，為全等的正三角形，且平面平面，平面平面，.

證明：；

求點(diǎn)到平面的距離.

Answer 1

【答案】證明見(jiàn)解析；.

【解析】

分別取,中點(diǎn),，連接,,，由題中的面面垂直可得平面，平面，從而得四邊形為平行四邊形，進(jìn)而可得證；

點(diǎn)到平面的距離與三棱錐的高相等，進(jìn)而利用等體積法計(jì)算即可求得距離.

解：證明：分別取,中點(diǎn),，連接,,，

，為全等的正三角形，

，.

平面平面，平面平面，且平面平面，平面平面，

平面，平面，.

又，

四邊形為平行四邊形.

.

，

.

記點(diǎn)到平面的距離為，由圖可知點(diǎn)到平面的距離與三棱錐的高相等，而三棱錐的體積與三棱錐的體積相同.

，，的邊長(zhǎng)為，，

，

三棱錐的體積.

在梯形中，，,

梯形的高為，.

由等體積法可知，，

，即.

故點(diǎn)點(diǎn)到平面的距離為.