
【題目】已知函數![]() ,且
,且![]() 在
在![]() 處的切線與
處的切線與![]() 平行.
平行.
![]() 求
求![]() 的單調區間;
的單調區間;
![]() 若存在區間
若存在區間![]() ,使
,使![]() 在
在![]() 上的值域是
上的值域是![]() ,求b的取值范圍.
,求b的取值范圍.
【答案】(1)見解析![]() .
.
【解析】
![]() 對函數
對函數![]() 求導,由
求導,由![]() 求出a的值,然后將a的值代入導數,求出極值點,討論導數的正負,即可求出函數
求出a的值,然后將a的值代入導數,求出極值點,討論導數的正負,即可求出函數![]() 的單調區間;
的單調區間;![]() 由函數
由函數![]() 在區間
在區間![]() 上單調遞增得到
上單調遞增得到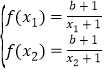 ,將問題轉化為關于x的方程
,將問題轉化為關于x的方程![]() 在區間
在區間![]() 上有兩個解,利用參變量分離法得出
上有兩個解,利用參變量分離法得出![]() 在區間
在區間![]() 上有兩個解,構造函數
上有兩個解,構造函數![]() ,利用導數研究函數
,利用導數研究函數![]() 的單調性與極值,作出函數
的單調性與極值,作出函數![]() 在區間
在區間![]() 上的圖象,即可求出b的取值范圍.
上的圖象,即可求出b的取值范圍.
![]() 由
由![]() ,得
,得![]() ,
,
由![]() ,得
,得![]() .
.
![]() .
.
則![]() ,
,
由![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() .
.
![]() 的單調減區間為
的單調減區間為![]() ,增區間為
,增區間為![]() ;
;
![]() 由
由![]() 知,
知,![]() ,且函數
,且函數![]() 在區間
在區間![]() 上單調遞增,若存在區間
上單調遞增,若存在區間![]() ,使
,使![]() 在
在![]() 上的值域是
上的值域是![]() ,
,
則有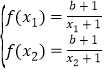 ,則
,則![]() ,得
,得![]() ,
,
所以,關于x的方程![]() 在區間
在區間![]() 上有兩解,
上有兩解,
由![]() ,得
,得![]() ,構造函數
,構造函數![]() ,其中
,其中![]() ,
,
所以,直線![]() 與函數
與函數![]() 的圖象在區間
的圖象在區間![]() 上有兩個交點,
上有兩個交點,
![]() ,
,
構造函數![]() ,則
,則![]() ,
,
所以,函數![]() 在區間
在區間![]() 上單調遞增,由于
上單調遞增,由于![]() ,
,
當![]() 時,
時,![]() ,即
,即![]() ;當
;當![]() 時,
時,![]() ,即
,即![]() .
.
所以,函數![]() 在區間
在區間![]() 上單調遞減,在區間
上單調遞減,在區間![]() 上單調遞增,
上單調遞增,
所以,函數![]() 在
在![]() 處取得最小值,即
處取得最小值,即![]() ,
,
由于![]() ,
,![]() ,所以,
,所以,![]() ,
,
結合圖象可知,當![]() 時,直線
時,直線![]() 與函數
與函數![]() 在區間
在區間![]() 上的圖象有兩個交點,
上的圖象有兩個交點,
因此,實數b的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足a1=1,an+1=![]() ,設bn=
,設bn=![]() ,n∈N*。
,n∈N*。
(1)證明{bn}是等比數列(指出首項和公比);
(2)求數列{log2bn}的前n項和Tn。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著我國經濟的發展,居民的儲蓄存款逐年增長.設某地區城鄉居民人民幣儲蓄存款(年底余額)如下表:
年 份 | 2013 | 2014 | 2015 | 2016 | 2017 |
時間代號t | 1 | 2 | 3 | 4 | 5 |
儲蓄存款y/千億元 | 5 | 6 | 7 | 8 | 10 |
(1)求y關于t的線性回歸方程![]() t+
t+![]() ;
;
(2)用所求回歸方程預測該地區2018年(t=6)的人民幣儲蓄存款.
附:回歸方程![]() t+
t+![]() 中,
中, .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列問題中,最適合用簡單隨機抽樣方法抽樣的是( )
A.某縣從該縣中、小學生中抽取200人調查他們的視力情況
B.從15種疫苗中抽取5種檢測是否合格
C.某大學共有學生5600人,其中專科生有1300人、本科生3000人、研究生1300人,現抽取樣本量為280的樣本調查學生利用因特網查找學習資料的情況,
D.某學校興趣小組為了了解移動支付在大眾中的熟知度,要對![]() 歲的人群進行隨機抽樣調查
歲的人群進行隨機抽樣調查
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】水葫蘆原產于巴西,![]() 年作為觀賞植物引入中國. 現在南方一些水域水葫蘆已泛濫成災嚴重影響航道安全和水生動物生長. 某科研團隊在某水域放入一定量水葫蘆進行研究,發現其蔓延速度越來越快,經過
年作為觀賞植物引入中國. 現在南方一些水域水葫蘆已泛濫成災嚴重影響航道安全和水生動物生長. 某科研團隊在某水域放入一定量水葫蘆進行研究,發現其蔓延速度越來越快,經過![]() 個月其覆蓋面積為
個月其覆蓋面積為![]() ,經過
,經過![]() 個月其覆蓋面積為
個月其覆蓋面積為![]() . 現水葫蘆覆蓋面積
. 現水葫蘆覆蓋面積![]() (單位
(單位![]() )與經過時間
)與經過時間![]() 個月的關系有兩個函數模型
個月的關系有兩個函數模型![]() 與
與![]() 可供選擇.
可供選擇.
(參考數據:![]() )
)
(Ⅰ)試判斷哪個函數模型更合適,并求出該模型的解析式;
(Ⅱ)求原先投放的水葫蘆的面積并求約經過幾個月該水域中水葫蘆面積是當初投放的![]() 倍.
倍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(理)某電視臺舉辦的闖關節目共有五關,只有通過五關才能獲得獎金,規定前三關若有失敗即結束,后兩關若有失敗再給一次從失敗的關開始繼續向前闖的機會(后兩關總共只有一次機會),已知某人前三關每關通過的概率都是![]() ,后兩關每關通過的概率都是
,后兩關每關通過的概率都是![]() .
.
(1)求該人獲得獎金的概率;
(2)設該人通過的關數為X,求隨機變量X的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知圓C:![]() .
.
![]() 若圓C的切線l在x軸和y軸上的截距相等,且截距不為零,求切線l的方程;
若圓C的切線l在x軸和y軸上的截距相等,且截距不為零,求切線l的方程;
![]() 已知點
已知點![]() 為直線
為直線![]() 上一點,由點P向圓C引一條切線,切點為M,若
上一點,由點P向圓C引一條切線,切點為M,若![]() ,求點P的坐標.
,求點P的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,![]() 、
、![]() 是以
是以![]() 為直徑的圓上兩點,
為直徑的圓上兩點,![]() ,
,![]() ,
,![]() 是
是![]() 上一點,且
上一點,且![]() ,將圓沿直徑
,將圓沿直徑![]() 折起,使點
折起,使點![]() 在平面
在平面![]() 的射影
的射影![]() 在
在![]() 上,已知
上,已知![]() .
.

(1)求證:![]() ⊥平面
⊥平面![]() ;
;
(2)求證:![]()
![]() 平面
平面![]() ;
;
(3)求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com