
【題目】已知等差數列前三項為a,4,3a,前n項的和為Sn , 若Sk=90.
(1)求a及k的值;
(2)設bn= ![]() ,求數列{bn}的前n項和.
,求數列{bn}的前n項和.
【答案】
(1)解:等差數列為{an}的前三項分別為:a1=a,a2=4,a3=3a,
∴a+3a=2×4,解得:a1=a=2,公差d=a2﹣a1=2,將Sk=90,
代入公式Sk=ka1+ ![]() ,解得:k=9,
,解得:k=9,
∴a=2,k=9
(2)解:由 (1)可知:Sn=2n+ ![]() ×2=n(n+1),
×2=n(n+1),
bn= ![]() =
= ![]() =
= ![]() ﹣
﹣ ![]() ,
,
數列{bn}的前n項和 ![]() +
+ ![]() +…+
+…+ ![]() =
= ![]() +
+ ![]() +…+
+…+ ![]() ,
,
=(1﹣ ![]() )+(
)+( ![]() ﹣
﹣ ![]() )+…+(
)+…+( ![]() ﹣
﹣ ![]() ),
),
=1﹣ ![]() ,
,
= ![]() ,
,
數列{bn}的前n項和 ![]()
【解析】(1)由等差數列的性質可知:a+3a=2×4,即可求得a1=a=2,d=a2﹣a1=2,代入前n項和公式即可求得k的值;(2)由bn= ![]() =
= ![]() =
= ![]() ﹣
﹣ ![]() ,采用“裂項法”即可求得數列{bn}的前n項和.
,采用“裂項法”即可求得數列{bn}的前n項和.
【考點精析】本題主要考查了等差數列的通項公式(及其變式)和數列的前n項和的相關知識點,需要掌握通項公式:![]() 或
或![]() ;數列{an}的前n項和sn與通項an的關系
;數列{an}的前n項和sn與通項an的關系 才能正確解答此題.
才能正確解答此題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】一個四棱錐的三視圖如圖所示,關于這個四棱錐,下列說法正確的是( )

A. 最長的棱長為![]()
B. 該四棱錐的體積為![]()
C. 側面四個三角形都是直角三角形
D. 側面三角形中有且僅有一個等腰三角形
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨機抽取某中學甲乙兩班各6名同學,測量他們的身高(單位:cm),獲得身高數據的莖葉圖如圖,則甲班樣本數據的眾數和乙班樣本數據的中位數分別是( ) 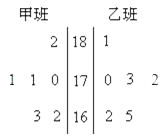
A.170,170
B.171,171
C.171,170
D.170,172
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若數列{an}是等差數列,首項a1>0,a2003+a2004>0,a2003 . a2004<0,則使前n項和Sn>0成立的最大自然數n是( )
A.4005
B.4006
C.4007
D.4008
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數y=f(x)是定義在(0,+∞)上的函數,并且滿足下面三個條件: ①對任意正數x,y,都有f(xy)=f(x)+f(y);
②當x>1時,f(x)>0;
③f(3)=1,
(1)求f(1), ![]() 的值;
的值;
(2)判斷函數f(x)在區間(0,+∞)上單調性,并用定義給出證明;
(3)對于定義域內的任意實數x,f(kx)+f(4﹣x)<2(k為常數,且k>0)恒成立,求正實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中,正確的是:( )
A. 命題“若![]() ,則
,則![]() ”的否命題為“若
”的否命題為“若![]() ,則
,則![]() ”
”
B. 命題“存在![]() ,使得
,使得![]() ”的否定是:“任意
”的否定是:“任意![]() ,都有
,都有![]() ”
”
C. 若命題“非![]() ”與命題“
”與命題“![]() 或
或![]() ”都是真命題,那么命題
”都是真命題,那么命題![]() 一定是真命題
一定是真命題
D. 命題“若![]() ,則
,則![]() ”的逆命題是真命題
”的逆命題是真命題
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知命題p:“ ![]() =1是焦點在x軸上的橢圓的標準方程”,命題q:“不等式組
=1是焦點在x軸上的橢圓的標準方程”,命題q:“不等式組  所表示的區域是三角形”.若p∨q為真命題,p∧q為假命題,求實數m的取值范圍.
所表示的區域是三角形”.若p∨q為真命題,p∧q為假命題,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
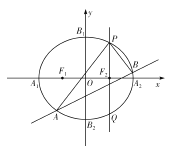
【題目】如圖,已知橢圓![]() 的左、右頂點分別為
的左、右頂點分別為![]() ,上、下頂點分別為
,上、下頂點分別為![]() ,兩個焦點分別為
,兩個焦點分別為![]() ,
, ![]() ,四邊形
,四邊形![]() 的面積是四邊形
的面積是四邊形![]() 的面積的2倍.
的面積的2倍.
(1)求橢圓![]() 的方程;
的方程;
(2)過橢圓![]() 的右焦點且垂直于
的右焦點且垂直于![]() 軸的直線交橢圓
軸的直線交橢圓![]() 于
于![]() 兩點,
兩點, ![]() 是橢圓
是橢圓![]() 上位于直線
上位于直線![]() 兩側的兩點.若
兩側的兩點.若![]() ,求證:直線
,求證:直線![]() 的斜率
的斜率![]() 為定值.
為定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com