
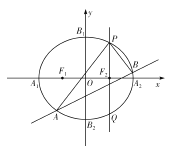
【題目】如圖,已知橢圓![]() 的左、右頂點分別為
的左、右頂點分別為![]() ,上、下頂點分別為
,上、下頂點分別為![]() ,兩個焦點分別為
,兩個焦點分別為![]() ,
, ![]() ,四邊形
,四邊形![]() 的面積是四邊形
的面積是四邊形![]() 的面積的2倍.
的面積的2倍.
(1)求橢圓![]() 的方程;
的方程;
(2)過橢圓![]() 的右焦點且垂直于
的右焦點且垂直于![]() 軸的直線交橢圓
軸的直線交橢圓![]() 于
于![]() 兩點,
兩點, ![]() 是橢圓
是橢圓![]() 上位于直線
上位于直線![]() 兩側的兩點.若
兩側的兩點.若![]() ,求證:直線
,求證:直線![]() 的斜率
的斜率![]() 為定值.
為定值.
【答案】(1)![]() ;(2)見解析
;(2)見解析
【解析】試題分析:(1) 因為![]() ,所以
,所以![]() ,①由四邊形
,①由四邊形![]() 的面積是四邊形
的面積是四邊形![]() 的面積的2倍,可得
的面積的2倍,可得![]() .② 聯立 ①② 解出a,b,c(2)由(1)易知點
.② 聯立 ①② 解出a,b,c(2)由(1)易知點![]() 的坐標分別為
的坐標分別為![]() 若
若![]() ,所以直線
,所以直線![]() 的斜率之和為0. 設直線
的斜率之和為0. 設直線![]() 的斜率為
的斜率為![]() ,則直線
,則直線![]() 的斜率為
的斜率為![]() ,
, ![]() ,
,
直線![]() 的方程為
的方程為![]() ,由
,由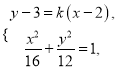 可得
可得![]() ,∴
,∴![]() ,同理直線
,同理直線![]() 的方程為
的方程為![]() ,
,
可得![]() ,∴
,∴![]() ,
,
![]()
![]() 把上邊式子代入即得解.
把上邊式子代入即得解.
試題解析:
(1)因為![]() ,所以
,所以![]() ,①
,①
由四邊形![]() 的面積是四邊形
的面積是四邊形![]() 的面積的2倍,
的面積的2倍,
可得![]() .②
.②
由①可得![]() ,所以
,所以![]() ,所以
,所以![]() .
.
所以橢圓![]() 的方程為
的方程為![]() .
.
(2)由(1)易知點![]() 的坐標分別為
的坐標分別為![]() 若
若![]() ,所以直線
,所以直線![]() 的斜率之和為0.
的斜率之和為0.
設直線![]() 的斜率為
的斜率為![]() ,則直線
,則直線![]() 的斜率為
的斜率為![]() ,
, ![]() ,
,
直線![]() 的方程為
的方程為![]() ,由
,由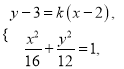
可得![]() ,∴
,∴![]() ,
,
同理直線![]() 的方程為
的方程為![]() ,
,
可得![]() ,∴
,∴![]() ,
,
![]()
![]() .
.


 口算題天天練系列答案
口算題天天練系列答案科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C的對邊分別為a,b,c,滿足:a2+c2=b2+ ![]() ac
ac
(1)求∠B 的大小;
(2)求 ![]() cosA+cosC 的最大值.
cosA+cosC 的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙、丙、丁四個物體同時從某一點出發向同一個方向運動,其路程fi(x)(i=1,2,3,4)關于時間x(x≥0)的函數關系式分別為f1(x)=2x﹣1,f2(x)=x3 , f3(x)=x,f4(x)=log2(x+1),有以下結論: ①當x>1時,甲走在最前面;
②當x>1時,乙走在最前面;
③當0<x<1時,丁走在最前面,當x>1時,丁走在最前面;
④丙不可能走在最前面,也不可能走在最后面;
⑤如果它們一直運動下去,最終走在最前面的是甲.
其中,正確結論的序號為(把正確結論的序號都填上,多填或少填均不得分)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2016年6月22 日,“國際教育信息化大會”在山東青島開幕.為了解哪些人更關注“國際教育信息化大會”,某機構隨機抽取了年齡在15-75歲之間的100人進行調查,并按年齡繪制成頻率分布直方圖,如圖所示,其分組區間為: ![]() .把年齡落在區間
.把年齡落在區間![]() 和
和![]() 內的人分別稱為 “青少年”和“中老年”.
內的人分別稱為 “青少年”和“中老年”.
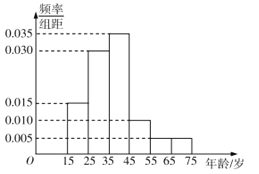
(1)根據頻率分布直方圖求樣本的中位數(保留兩位小數)和眾數;
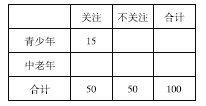
(2)根據已知條件完成下面的![]() 列聯表,并判斷能否有
列聯表,并判斷能否有![]() 的把握認為“中老年”比“青少年”更加關注“國際教育信息化大會”;
的把握認為“中老年”比“青少年”更加關注“國際教育信息化大會”;
附:參考公式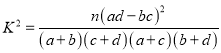 ,其中
,其中![]() .
.
臨界值表:
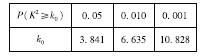
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知圓心坐標為( ![]() ,1)的圓M與x軸及直線y=
,1)的圓M與x軸及直線y= ![]() x分別相切于A,B兩點,另一圓N與圓M外切、且與x軸及直線y=
x分別相切于A,B兩點,另一圓N與圓M外切、且與x軸及直線y= ![]() x分別相切于C、D兩點.
x分別相切于C、D兩點. 
(1)求圓M和圓N的方程;
(2)過點B作直線MN的平行線l,求直線l被圓N截得的弦的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市對創“市級優質學校”的甲、乙兩所學校復查驗收,對辦學的社會滿意度一項評價隨機訪問了![]() 位市民,根據這
位市民,根據這![]() 位市民對這兩所學校的評分(評分越高表明市民的評價越好),繪制莖葉圖如下:
位市民對這兩所學校的評分(評分越高表明市民的評價越好),繪制莖葉圖如下:
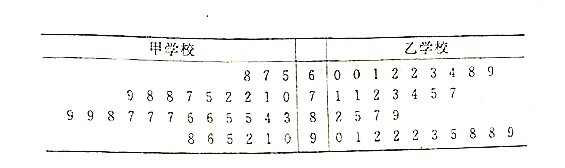
(1)分別估計該市的市民對甲、乙兩所學校評分的中位數;
(2)分別估計該市的市民對甲、乙兩所學校的評分不低于![]() 分的概率;
分的概率;
(3)根據莖葉圖分析該市的市民對甲、乙兩所學校的評價.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com