Question

【題目】設函數y=f（x）是定義在（0，+∞）上的函數，并且滿足下面三個條件： ①對任意正數x，y，都有f（xy）=f（x）+f（y）；
②當x＞1時，f（x）＞0；
③f（3）=1，
（1）求f（1）， 的值；
（2）判斷函數f（x）在區間（0，+∞）上單調性，并用定義給出證明；
（3）對于定義域內的任意實數x，f（kx）+f（4﹣x）＜2（k為常數，且k＞0）恒成立，求正實數k的取值范圍．

Answer 1

【答案】
（1）解：令x=y=1，得f（1）=0，令x=3， ，

則 ，所以

（2）解：函數f（x）在區間（0，+∞）上單調遞增，證明如下

任取x1，x2∈（0，+∞），且x1＜x2，

則f（x1）﹣f（x2）= ，

因為x1，x2∈（0，+∞），且x1＜x2，則 ，又x＞1時，f（x）＞0，

所以 ，即f（x1）＜f（x2），

函數f（x）在區間（0，+∞）上單調遞增

（3）解：f（9）=f（3）+f（3）=2，

由（2）知函數f（x）在區間（0，+∞）上單調遞增

不等式f（kx）+f（4﹣x）＜2可化為f（kx（4﹣x））＜f（9），因為k＞0

不等式故可化為 ，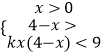

由題可得，0＜x＜4時，kx（4﹣x）＜9恒成立，

即0＜x＜4時， 恒成立， 0＜x＜4，y=x（4﹣x）∈（0，4]，

所以

所以

【解析】（1）利用賦值法即可求f（1）， 的值；（2）根據函數單調性的定義即可判斷函數f（x）在區間（0，+∞）上單調性；（3）根據函數奇偶性和單調性的性質將不等式進行轉化求解即可．