
科目: 來源:學習周報 數學 華師大八年級版 2009-2010學年 第18期 總第174期 華師大版 題型:044
一種電訊信號轉發裝置的發射直徑為31 km.現要求在一邊長為30 km的正方形城區選擇若干個安裝點,每個點安裝一個這種轉發裝置,使這些裝置轉發的信號能完全覆蓋這個城市.問:
(1)能否找到這樣的4個安裝點,使得這些點安裝了這種轉發裝置后能達到預設的要求?
(2)至少需要選擇多少個安裝點,才能使這些點安裝了這種轉發裝置后達到預設的要求?
答題要求:請在解答時,畫出必要的示意圖,并用必要的計算、推理和文字來說明你的理由.(圖給出了幾個邊長為30 km的正方形城區示意圖,供解題時選用)

查看答案和解析>>
科目: 來源:學習周報 數學 滬科九年級版 2009-2010學年 第19期 總第175期 滬科版 題型:044
一位小朋友在不打滑的平面軌道上滾動一個半徑為
10 cm的圓盤,當滾動到與坡面BC開始相切時停止.其中AB=80 cm,BC與水平面的夾角為60°.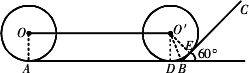
(1)求出圓盤在AB上滾動一圈時,其圓心所經過的路線的長度(π取3.14);
(2)當圓盤從點A滾動到與BC開始相切時停止,其圓心所經過的路線長大約是多少(精確到0.1 cm)?
查看答案和解析>>
科目: 來源:學習周報 數學 滬科九年級版 2009-2010學年 第17期 總第173期 滬科版 題型:044
如圖,⊙
O是△ABC的外接圓,∠BAC與∠ABC的平分線相交于點I,延長AI交⊙O于點D,連接BD、DC.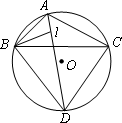
(1)求證:BD=DC=DI;
(2)若⊙O的半徑為10 cm,∠BAC=120°,求△BDC的面積.
查看答案和解析>>
科目: 來源:學習周報 數學 滬科九年級版 2009-2010學年 第15期 總第171期 滬科版 題型:044
如圖,已知
A、B、C、D是⊙O上的四個點,AB=BC,BD交AC于點E,連接CD、AD.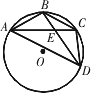
(1)求證:DB平分∠ADC;
(2)若BE=3,ED=6,求AB的長.
查看答案和解析>>
科目: 來源:學習周報 數學 滬科九年級版 2009-2010學年 第14期 總第170期 滬科版 題型:044
把兩個全等的等腰直角三角板
ABC和EFG(其直角邊長均為4)疊放在一起(如圖a),且使三角板EFG的直角頂點G與三角板ABC斜邊的中點O重合.現將三角板EFG繞點O順時針旋轉α(旋轉角α滿足條件:0°<α<90°),如圖b,四邊形CHGK是旋轉過程中兩個三角板的重疊部分.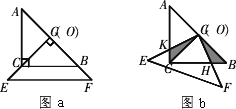
在上述旋轉過程中,
BH與CK有怎樣的數量關系?重疊部分的面積有何變化?請證明你的發現.查看答案和解析>>
科目: 來源:學習周報 數學 滬科九年級版 2009-2010學年 第13期 總第169期 滬科版 題型:044
已知某種水果的批發單價與批發量的函數關系如圖所示.
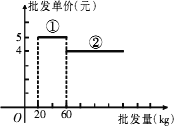
(1)請說明上圖中①、②兩段函數圖象的實際意義;
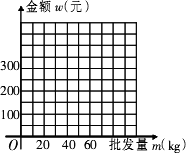
(2)寫出批發該種水果的資金金額w(元)與批發量m(kg)之間的函數關系式;在下圖的坐標系中畫出該函數圖象;指出金額在什么范圍內,以同樣的資金可以批發到較多數量的該種水果;
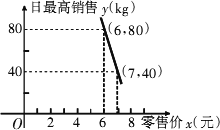
(3)經調查,某經銷商銷售該種水果的日最高銷量y與零售價x之間的函數關系如圖所示,該經銷商擬每日售出60 kg以上該種水果,且當日零售價不變,請你幫助該經銷商設計進貨和銷售的方案,使得當日獲得的利潤W最大.
查看答案和解析>>
科目: 來源:學習周報 數學 滬科九年級版 2009-2010學年 第13期 總第169期 滬科版 題型:044
如下圖,有一個呈直角三角形的不銹鋼片,已知∠
C=90°,AB=5 cm,BC=3 cm.試設計一種方案,用這個不銹鋼片裁出一個面積最大的正方形,并求出它的面積.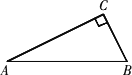
查看答案和解析>>
科目: 來源:學習周報 數學 滬科九年級版 2009-2010學年 第12期 總第168期 滬科版 題型:044
如圖,足球場上守門員從點
O處開出一高球,球從離地面1米的A處飛出(A在y軸上),運動員乙在距點O6米的B處發現球在自己頭的正上方達到最高點M,距地面約4米高,球落地后又一次彈起.據實驗測算,足球在草坪上彈起后的拋物線與原來的拋物線形狀相同,最大高度減少到原來最大高度的一半.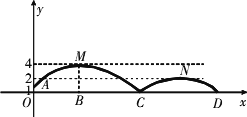
(1)求足球開始飛出到第一次落地時,該拋物線的函數關系式;
(2)足球第一次落地點C距守門員約多少米(取4![]() ≈7)?
≈7)?
(3)運動員乙要搶到第二個落地點D,他應再向前跑多少米(取2![]() ≈5)?
≈5)?
查看答案和解析>>
科目: 來源:學習周報 數學 滬科九年級版 2009-2010學年 第12期 總第168期 滬科版 題型:044
善于不斷改進學習方法的小虎發現,對解題進行回顧反思,學習效果會更好.某一天小虎有
20分鐘時間可用于學習.假設小虎解題的學習收益量y1與用于解題的時間x1(單位:分鐘)的關系如圖1所示,回顧反思的學習收益量y2與用于回顧反思的時間x2(單位:分鐘)的關系如圖2所示(其中OA是拋物線的一部分,A為拋物線的頂點),且用于回顧反思的時間不超過用于解題的時間.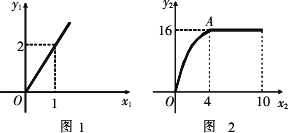
(1)求小虎解題的學習收益量y1與用于解題的時間x1之間的函數關系式;
(2)求小虎回顧反思的學習收益量y2與用于回顧反思的時間x2的函數關系式;
(3)問小虎如何分配解題和回顧反思的時間,才能使這20分鐘的學習收益總量最大?最大值為多少?
查看答案和解析>>
科目: 來源:學習周報 數學 滬科九年級版 2009-2010學年 第12期 總第168期 滬科版 題型:044
如圖,某公路隧道橫截面為拋物線,其最大高度為
6米,底部寬度OM為12米.現以點O為原點,OM所在直線為x軸建立直角坐標系.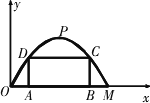
(1)直接寫出點M及拋物線的頂點P的坐標;
(2)求這條拋物線的函數關系式;
(3)若要搭建一個矩形“支撐架”AD-DC-CB,使C、D兩點在拋物線上,A、B兩點在地面OM上,則這個“支撐架”總長的最大值是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com