
科目: 來源:1+1輕巧奪冠·優化訓練·八年級數學下 題型:044
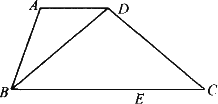
如圖,在梯形ABCD中,AD∥BC,BD=CD,AB<CD,且∠ABC為銳角.若AD=4,BC=12,E為BC上一點.
問:當CE分別為何值時,四邊形ABED是等腰梯形?直角梯形?請分別說明理由.
查看答案和解析>>
科目: 來源:1+1輕巧奪冠·優化訓練·八年級數學下 題型:044
已知:如圖,在直角梯形ABCD中,AD∥BC,BC=5 cm,CD=6 cm,∠DCB=60°,∠ABC=90°.等邊三角形MPN(N為不動點)的邊長為a cm,邊MN和直角梯形ABCD的底邊BC都在直線l上,NC=8 cm.將直角梯形ABCD向左翻折180°,翻折一次得到圖形①,翻折兩次得圖形②,如此翻折下去.
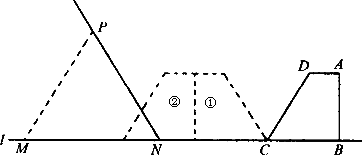
(1)將直角梯形ABCD向左翻折兩次,如果此時等邊三角形的邊長a≥2 cm,則兩圖形重疊部分的面積是多少?
(2)將直角梯形ABCD向左翻折三次,如果第三次翻折得到的直角梯形與等邊三角形重疊部分的面積等于直角梯形ABCD的面積,這時等邊三角形的邊長a至少應為多少?
(3)將直角梯形ABCD向左翻折三次,如果第三次翻折得到的直角梯形與等邊三角形重疊部分的面積等于直角梯形面積的一半,這時等邊三角形的邊長應為多少?
查看答案和解析>>
科目: 來源:同步輕松練習 九年級數學下 題型:044
臺風是一種自然災害,它以臺風中心為圓心在周圍數十千米范圍內形成氣旋風暴,有極強的破壞力.據氣象觀測,距沿海某城市A的正南方向220 km的B處有一臺風中心.其中心最大風力為12級,每遠離臺風中心20 km,風力就會減弱一級,該臺風中心正以15 km/h的速度沿北偏東30°方向往C移動,且臺風中心風力不變,如圖所示.若城市所受風力達到或超過4級,則稱為受臺風影響.
(1)該城市是否會受到這次臺風的影響?請說明理由;
(2)若會受臺風影響,那么臺風影響該城市的持續時間有多長?
(3)該城市受到臺風影響的最大風力為幾級?
查看答案和解析>>
科目: 來源:同步輕松練習 九年級數學下 題型:044
如圖,在一半徑為168 cm的半圓形障礙物前600 cm處有一豎直的柱子.已知落在半圓上的影長為56π cm,同時,一直立70 cm桿子的影長為171 cm,求柱子的高度.(結果精確到1 cm.)

查看答案和解析>>
科目: 來源:同步輕松練習 九年級數學下 題型:044
如圖,五一期間在某商貿大廈上從點A到點B懸掛了一條宣傳條幅,小明和小雯的家正好住在商貿大廈對面的家屬樓上.小明在四樓D點測得條幅端點A的仰角為30°,測得條幅端點B的俯角為45°;小雯在三樓C點測得條幅端點A的仰角為45°,測得條幅端點B的俯角為30°.若設樓層高度CD為3 m,請你根據小明和小雯測得的數據求出條幅AB的長.(參考數據:![]() ≈1.732,結果精確到1 m.)
≈1.732,結果精確到1 m.)

查看答案和解析>>
科目: 來源:同步輕松練習 九年級數學下 題型:044
一段路基的橫斷面是直角梯形,如甲圖所示,已知原來坡面的坡角α的正弦值為0.6,現不改變土石方量,全部利用原有土石方進行坡面改造,使坡度變小,達到如乙圖所示的技術要求.試求出改造后坡面的坡度是多少?
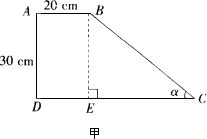
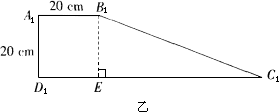
查看答案和解析>>
科目: 來源:同步輕松練習 九年級數學下 題型:044
某課外學習小組在設計一個長方形時鐘鐘面時,欲使長方形的寬為20 cm,時鐘的中心在長方形對角線的交點上,數字2在長方形的頂點上,數字3,6,9,12標在所在邊的中點上,如圖所示.
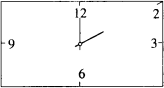
(1)問長方形的長應為多少?
(2)請你在長方框上點出數字1的位置,并說明確定該位置的方法;
(3)請你在長方框上點出鐘面上其余數字的位置,并寫出相應的數字(說明:要畫出必要的、反映解題思路的輔助線).
查看答案和解析>>
科目: 來源:同步輕松練習 九年級數學下 題型:044
在△ABC中,∠A,∠B,∠C所對的邊分別用a,b,c表示.
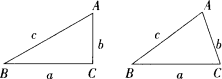
(1)如圖,在△ABC中,∠A=2∠B,且∠A=60°.求證:a2=b(b+c);
(2)如果一個三角形的一個內角等于另一個內角的2倍,我們稱這樣的三角形為“倍角三角形”.本題第一問中的三角形是一個特殊的倍角三角形,那么對于任意的倍角三角形ABC,其中∠A=2∠B,關系式a2=b(b+c)是否仍然成立?請證明你的結論.
查看答案和解析>>
科目: 來源:同步輕松練習 九年級數學下 題型:044
某種吊車的車身高EF=2 m,吊車臂AE=24 m,現要把如圖①所示的圓柱形裝飾物吊到14 m高的屋頂上安裝.吊車在吊起的過程中,圓柱形的裝飾物始終保持水平,如圖②,若吊車臂與水平方向的夾角為59°,問能否吊裝成功?(參考數據:sin59°≈0.8572,cos59°≈0.5150,tan59°≈1.6643.)
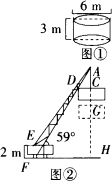
查看答案和解析>>
科目: 來源:同步輕松練習 九年級數學下 題型:044
如圖,某海濱浴場的沿岸可以看作直線,1號救生員在岸邊的A點看到海中的B點有人求救,便立即向前跑300 m到離B點最近的D點,再跳入海中游到B點救助;若每位救生員在岸上跑步的速度都是6 m/s,在水中游泳的速度都是2 m/s,∠BAD=45°.

(1)請問1號救生員的做法是否合理?
(2)若2號救生員從A跑到C,再跳入海中游到B點救助,且∠BCD=65°,請問誰先到達點B?(參考數據:sin65°≈0.9,cos65°≈0.4,tan65°≈2,![]() ≈1.4,結果精確到0.1 m.)
≈1.4,結果精確到0.1 m.)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com