
分析 由于ax12+bx1=ax22+bx2,移項(xiàng)后分解得到(x1-x2)(ax1+ax2+b)=0,而x1≠x2,所以ax1+ax2+b=0,即x1+x2=-$\frac{b}{a}$,然后把x=-$\frac{b}{a}$代入二次函數(shù)解析式中計(jì)算即可.
解答 0解:根據(jù)題意得ax12+bx1=ax22+bx2,
ax12-ax22+bx1-bx2=0,
a(x1-x2)(x1+x2)+b(x1-x2)=0,
(x1-x2)(ax1+ax2+b)=0,
∵x1≠x2,
∴ax1+ax2+b=0,即x1+x2=-$\frac{b}{a}$,
∴當(dāng)x=x1+x2=-$\frac{b}{a}$時(shí),y=a×(-$\frac{b}{a}$)2+b×(-$\frac{b}{a}$)=0.
故答案為0.
點(diǎn)評 本題考查了二次函數(shù)的性質(zhì):二次函數(shù)y=ax2+bx+c(a≠0)的頂點(diǎn)坐標(biāo)是(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),對稱軸直線x=-$\frac{b}{2a}$,二次函數(shù)y=ax2+bx+c(a≠0)的圖象具有如下性質(zhì):①當(dāng)a>0時(shí),拋物線y=ax2+bx+c(a≠0)的開口向上,當(dāng)x<-$\frac{b}{2a}$時(shí),y隨x的增大而減小;x>-$\frac{b}{2a}$時(shí),y隨x的增大而增大;x=-$\frac{b}{2a}$時(shí),y取得最小值$\frac{4ac-{b}^{2}}{4a}$,即頂點(diǎn)是拋物線的最低點(diǎn).②當(dāng)a<0時(shí),拋物線y=ax2+bx+c(a≠0)的開口向下,x<-$\frac{b}{2a}$時(shí),y隨x的增大而增大;x>-$\frac{b}{2a}$時(shí),y隨x的增大而減小;當(dāng)x=-$\frac{b}{2a}$時(shí),y取得最大值$\frac{4ac-{b}^{2}}{4a}$,即頂點(diǎn)是拋物線的最高點(diǎn).


 桃李文化快樂暑假武漢出版社系列答案
桃李文化快樂暑假武漢出版社系列答案 優(yōu)秀生快樂假期每一天全新寒假作業(yè)本系列答案
優(yōu)秀生快樂假期每一天全新寒假作業(yè)本系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
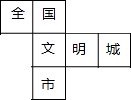 在市委、市政府的領(lǐng)導(dǎo)下,全市人民齊心協(xié)力,力爭于2017年將我市創(chuàng)建為“全國文明城市”,為此小宇特制了正方體模具,其展開圖如圖所示,原正方體中與“文”字所在的面正對面上標(biāo)的字是( )
在市委、市政府的領(lǐng)導(dǎo)下,全市人民齊心協(xié)力,力爭于2017年將我市創(chuàng)建為“全國文明城市”,為此小宇特制了正方體模具,其展開圖如圖所示,原正方體中與“文”字所在的面正對面上標(biāo)的字是( )| A. | 全 | B. | 國 | C. | 明 | D. | 城 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
 △ABC中,AB=AC,AD⊥BC,∠BAC=∠ACG=4∠EDC,CG=AD=4,$\frac{{{S_{△DEC}}}}{{{S_{△ACG}}}}$=$\frac{1}{4}$,BC=4$\sqrt{5}$.
△ABC中,AB=AC,AD⊥BC,∠BAC=∠ACG=4∠EDC,CG=AD=4,$\frac{{{S_{△DEC}}}}{{{S_{△ACG}}}}$=$\frac{1}{4}$,BC=4$\sqrt{5}$.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | x2+2x=x2-1 | B. | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$-2=0 | C. | ax2+bx+c=0 | D. | (x+1)2=2(x+1) |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
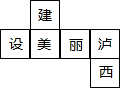 如圖是一個(gè)正方體的表面展開圖,則原正方體中與“建”字所在的面相對的面上標(biāo)的字是( )
如圖是一個(gè)正方體的表面展開圖,則原正方體中與“建”字所在的面相對的面上標(biāo)的字是( )| A. | 美 | B. | 麗 | C. | 瀘 | D. | 西 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com