
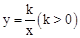 與它的其中一條對稱軸
與它的其中一條對稱軸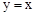 相交于兩點A,B,則線段AB的長稱為雙曲線
相交于兩點A,B,則線段AB的長稱為雙曲線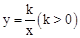 的對徑.
的對徑.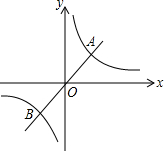
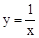 的對徑;
的對徑;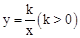 對徑是
對徑是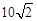 .求k的值;
.求k的值;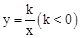 的對徑.
的對徑.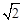 ;(2)25;(3)定義見解析.
;(2)25;(3)定義見解析.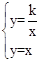 ,可得到A點坐標為(1,1),B點坐標為(-1,-1),即OC=AC=1,由勾股定理可求AB,于是得到雙曲線
,可得到A點坐標為(1,1),B點坐標為(-1,-1),即OC=AC=1,由勾股定理可求AB,于是得到雙曲線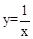 的對徑;
的對徑;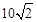 ,即AB=
,即AB=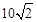 ,OA=5
,OA=5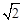 ,根據OA=
,根據OA=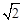 OC=
OC=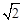 AC,則OC=AC=5,得到點A坐標為(5,5),把A(5,5)代入雙曲線
AC,則OC=AC=5,得到點A坐標為(5,5),把A(5,5)代入雙曲線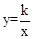 (k>0)即可得到k的值;(3)雙曲線
(k>0)即可得到k的值;(3)雙曲線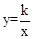 (k<0)的一條對稱軸與雙曲線有兩個交點,根據題目中的定義易得到雙曲線
(k<0)的一條對稱軸與雙曲線有兩個交點,根據題目中的定義易得到雙曲線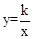 (k<0)的對徑.
(k<0)的對徑.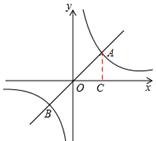
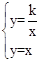 ,得
,得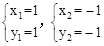 ,∴A點坐標為(1,1),B點坐標為(-1,-1).
,∴A點坐標為(1,1),B點坐標為(-1,-1).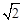 OC=
OC=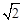 . ∴AB=2OA=2
. ∴AB=2OA=2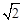 .
.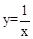 的對徑是2
的對徑是2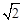 .
.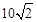 ,即AB=
,即AB=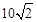 ,OA=5
,OA=5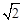 .
.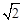 OC=
OC=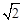 AC,∴OC=AC=5. ∴點A坐標為(5,5).
AC,∴OC=AC=5. ∴點A坐標為(5,5).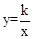 (k>0)得k=5×5=25,即k的值為25.
(k>0)得k=5×5=25,即k的值為25.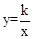 (k<0)與它的其中一條對稱軸y=-x相交于A、B兩點,則線段AB的長稱為雙曲線
(k<0)與它的其中一條對稱軸y=-x相交于A、B兩點,則線段AB的長稱為雙曲線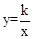 (k<0)的對徑.
(k<0)的對徑.

 學而優銜接教材南京大學出版社系列答案
學而優銜接教材南京大學出版社系列答案 小學課堂作業系列答案
小學課堂作業系列答案 金博士一點全通系列答案
金博士一點全通系列答案科目:初中數學 來源:不詳 題型:單選題
|
一輛汽車勻速通過某段公路,所需時間t(h)與行駛速度v(km/h)滿足函數關系:
 ,其圖象為如圖所示的一段曲線,且端點為 ,其圖象為如圖所示的一段曲線,且端點為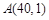 和 和 ,若行駛速度不得超過60(km/h),則汽車通過該路段最少需要時間為( ) ,若行駛速度不得超過60(km/h),則汽車通過該路段最少需要時間為( )
|
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
 經過第一、二、三象限,與y軸交于點B,點A(2,t)在這條直線上,連接AO,△AOB的面積等于1.
經過第一、二、三象限,與y軸交于點B,點A(2,t)在這條直線上,連接AO,△AOB的面積等于1.
 (
( 是常量,
是常量, )的圖像經過點A,求這個反比例函數的解析式.
)的圖像經過點A,求這個反比例函數的解析式.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com