Question

12．已知，如圖，平面直角坐標系xOy中，線段AB∥y軸，點B在x軸正半軸上，點A在第一象限，AB=10．點P是線段AB上的一動點，當點P在線段AB上從點A向點B開始運動時，點B同時在x軸上從點C（4，0）向點O運動，點P、點B運動的速度都是每秒1個單位，設(shè)運動的時間為t（0＜t＜4）．

（1）用含有t的式子表示點P的坐標；
（2）當點P恰好在直線y=3x上時，求線段AP的長；
（3）在（2）的條件下，直角坐標平面內(nèi)是否存在點D，使以O(shè)、P、A、D為頂點的四邊形是等腰梯形．如果存在，請直接寫出點D的坐標；如果不存在，請簡單說明理由．

Answer 1

分析 （1）由題意表示出BP，OB即可；
（2）由點P在直線y=3x上，建立方程求出t即可；
（3）分三種情況討論計算，①當AP，OD為底時，AP∥OD，AD=OP，AP≠OD，②當OP，AD為底時，AP=OD，OD不平行AP，OP∥AD③當DP，OA為底時，AP=OD，AP不平行OD，PD∥OA，即可．

解答 解：（1）根據(jù)題意得，BP=AB-AP=10-t，OB=OC-BC=4-t，
∴P（4-t，10-t），
（2）由（1）得，P（4-t，10-t），
∴將P（4-t，10-t）代入y=3x，得t=1，
∴AP=1，
（3）∵以O(shè)、P、A、D為頂點的四邊形是等腰梯形，
①如圖1，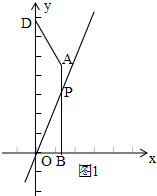

當AP，OD為底時，
∴AP∥OD，AD=OP，AP≠OD，
∴點D在y軸上，
設(shè)點D（0，a），
由（2）有，t=1，
∴A（3，10），P（3，9），
∴AD=$\sqrt{9+（{10-a）}^{2}}$，OP=$\sqrt{9+81}$
∴$\sqrt{9+（{10-a）}^{2}}$=$\sqrt{9+81}$，
∴a=19或a=1（∵AP=OD=1，∴舍）．
∴D（0，19），
②如圖2，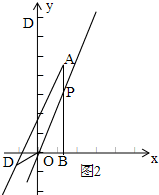

當OP，AD為底時，
∴AP=OD，OD不平行AP，OP∥AD
∵點P在直線y=3x上，且點A（3，10），
∴直線AD解析式為y=3x+1，
設(shè)D（b，3b+1），
由（2）有，t=1，
∴A（3，10），P（3，9），
∴AP=1，OD=$\sqrt{{b}^{2}+（3b+1）^{2}}$，
∴1=$\sqrt{{b}^{2}+（3b+1）^{2}}$，
∴b=-$\frac{3}{5}$或b=0（∵OD∥AP，∴舍），
∴D（-$\frac{3}{5}$，-$\frac{4}{5}$），
③如圖3，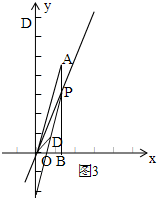

當DP，OA為底時，
∴AP=OD，AP不平行OD，PD∥OA，
∵A（3，10），
∴直線OA解析式為y=$\frac{10}{3}$x，
∵P（3，10），
∴直線PD解析式為y=$\frac{10}{3}$x-1，
設(shè)D（c，$\frac{10}{3}$c-1），
由（2）有，t=1，
∴A（3，10），P（3，9），
∴AP=1，OD=$\sqrt{{c}^{2}+（{\frac{10}{3}c-1）}^{2}}$，
∴1=$\sqrt{{c}^{2}+（{\frac{10}{3}c-1）}^{2}}$，
∴c=$\frac{60}{109}$或c=-1（∵AP∥OD，∴舍），
∴D（$\frac{60}{109}$，$\frac{91}{109}$），
∴符合條件的D（0，19）、（-$\frac{3}{5}$，-$\frac{4}{5}$）、（$\frac{60}{109}$，$\frac{91}{109}$）．

點評 此題是一次函數(shù)綜合題，主要考查了點在直線上的特點，待定系數(shù)法求函數(shù)解析式，等腰梯形的性質(zhì)，解本題的關(guān)鍵是分情況討論計算，難點是畫出滿足題意的圖形．