
 如圖,已知函數y=x+1的圖象與y軸交于點A,一次函數y=kx+b的圖象經過點B(0,-1),與x軸以及y=x+1的圖象分別交于點C、D,且點D的坐標為(1,n),
如圖,已知函數y=x+1的圖象與y軸交于點A,一次函數y=kx+b的圖象經過點B(0,-1),與x軸以及y=x+1的圖象分別交于點C、D,且點D的坐標為(1,n),分析 (1)對于直線y=x+1,令x=0求出y的值,確定出A的坐標,把B坐標代入y=kx+b中求出b的值,再將D坐標代入y=x+1求出n的值,進而將D坐標代入求出k的值即可;
(2)由兩一次函數解析式,結合圖象確定出x的范圍即可;
(3)過D作DE垂直于x軸,如圖1所示,四邊形AOCD面積等于梯形AOED面積減去三角形CDE面積,求出即可;
(4)在x軸上存在點P,使得以點P,C,D為頂點的三角形是直角三角形,理由為:分兩種情況考慮:①DP′⊥DC;②DP⊥CP,分別求出P坐標即可.
解答 解:(1)對于直線y=x+1,令x=0,得到y=1,即A(0,1),
把B(0,-1)代入y=kx+b中,得:b=-1,
把D(1,n)代入y=x+1得:n=2,即D(1,2),
把D坐標代入y=kx-1中得:2=k-1,即k=3,
故答案為:2,3,-1;
(2)∵一次函數y=x+1與y=3x-1交于D(1,2),
∴由圖象得:函數y=kx+b的函數值大于函數y=x+1的函數值時x的取值范圍是x>1;
故答案為:x>1;
(3)過D作DE⊥x軸,垂足為E,如圖1所示,
則S四邊形AOCD=S梯形AOED-S△CDE=$\frac{1}{2}$(AO+DE)•OE-$\frac{1}{2}$CE•DE=$\frac{1}{2}$×(1+2)×1-$\frac{1}{2}$×$\frac{2}{3}$×2=$\frac{3}{2}$-$\frac{2}{3}$=$\frac{5}{6}$;
(4)在x軸上存在點P,使得以點P,C,D為頂點的三角形是直角三角形,理由為:
如圖2所示,分兩種情況考慮: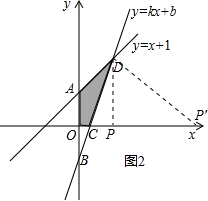
①當P′D⊥DC時,可得kP′D•kDC=-1,
∵直線DC斜率為3,
∴直線P′D斜率為-$\frac{1}{3}$,
∵D(1,2),
∴直線P′D解析式為y-2=-$\frac{1}{3}$(x-1),
令y=0,得到x=7,即P′(7,0);
②當DP⊥CP時,由D橫坐標為1,得到P橫坐標為1,
∵P在x軸上,
∴P的坐標為(1,0).
點評 此題屬于一次函數綜合題,涉及的知識有:一次函數與坐標軸的交點,直角三角形的性質,坐標與圖形性質,待定系數法確定一次函數解析式,利用了數形結合的思想,熟練掌握一次函數的性質是解本題的關鍵.


科目:初中數學 來源: 題型:解答題
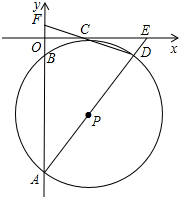 如圖,在平面直角坐標系中,⊙P經過x軸上一點C,與y軸分別交于A、B兩點,連接AP并延長分別交⊙P、x軸于點D、E,連接DC并延長交y軸于點F,若點F的坐標為(0,1),點D的坐標為(6,-1).
如圖,在平面直角坐標系中,⊙P經過x軸上一點C,與y軸分別交于A、B兩點,連接AP并延長分別交⊙P、x軸于點D、E,連接DC并延長交y軸于點F,若點F的坐標為(0,1),點D的坐標為(6,-1).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
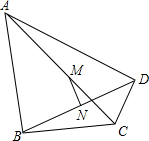 已知,如圖,∠ABC=∠ADC=90°,M、N分別是AC、BD的中點.
已知,如圖,∠ABC=∠ADC=90°,M、N分別是AC、BD的中點.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com