
如圖,在▱ABCD中,用直尺和圓規作∠BAD的平分線AG交BC于點E.若BF=6,AB=5,則AE的長為( )
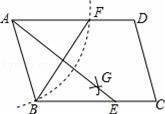

A.4 B.6 C.8 D.10
C【考點】平行四邊形的性質;等腰三角形的判定與性質;勾股定理;作圖—基本作圖.
【專題】計算題.
【分析】由基本作圖得到AB=AF,加上AO平分∠BAD,則根據等腰三角形的性質得到AO⊥BF,BO=FO=
 BF=3,再根據平行四邊形的性質得AF∥BE,所以∠1=∠3,于是得到∠2=∠3,根據等腰三角形的判定得AB=EB,然后再根據等腰三角形的性質得到AO=OE,最后利用勾股定理計算出AO,從而得到AE的長.
BF=3,再根據平行四邊形的性質得AF∥BE,所以∠1=∠3,于是得到∠2=∠3,根據等腰三角形的判定得AB=EB,然后再根據等腰三角形的性質得到AO=OE,最后利用勾股定理計算出AO,從而得到AE的長.
【解答】解:連結EF,AE與BF交于點O,如圖,
∵AB=AF,AO平分∠BAD,
∴AO⊥BF,BO=FO=
 BF=3,
BF=3,
∵四邊形ABCD為平行四邊形,
∴AF∥BE,
∴∠1=∠3,
∴∠2=∠3,
∴AB=EB,
而BO⊥AE,
∴AO=OE,
在Rt△AOB中,AO=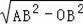
 =
=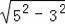
 =4,
=4,
∴AE=2AO=8.
故選C.
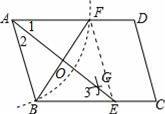

【點評】本題考查了平行四邊形的性質:平行四邊形的對邊相等;平行四邊形的對角相等;平行四邊形的對角線互相平分.也考查了等腰三角形的判定與性質和基本作圖.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:初中數學 來源: 題型:
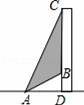
如圖,某高樓CD與處地面垂直,要在高樓前的地面A處安裝某種射燈,安裝后,射燈發出的光線與地面的最大夾角∠DAC為70°,光線與地面的最小夾角∠DAB為35°,要使射燈發光時照射在高樓上的區域寬BC為50米,求A處到高樓的距離AD.(結果精確到0.1米)
【參考數據:sin70°=0.94,cos70°=0.34,tan70°=2.75,sin35°=0.57,cos35°=0.82,tan35°=0.70】

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com