
分析 作CE∥AD交AB于E,則四邊形AECD是平行四邊形,∠CEB=∠BAD,得出AD=CE,證出AD=CD,再證明∠1=30°,證出∠B=∠CEB=60°,得出CE=BC=2,AD=CD=2,即可得出結果.
解答 解:作CE∥AD交AB于E,如圖所示: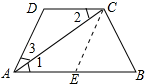
則四邊形AECD是平行四邊形,∠CEB=∠BAD,
∴AD=CE,
∵AB∥CD,
∴∠1=∠2,
∵AC平分∠BAD,
∴∠1=∠3,
∴∠2=∠3,
∴AD=CD,
∵AC⊥BC,BC=2,AB=4,
∴∠1=30°,
∴∠3=30°,∠B=90°-30°=60°,
∴∠CEB=∠BAD=30°+30°=60°,
∴∠B=∠CEB=60°,
∴CE=BC=2,
∴AD=CD=2,
∴梯形ABCD的周長=AB+BC+CD+AD=4+2+2+2=10.
故答案為:10.
點評 本題考查了梯形的性質、平行四邊形的判定與性質、等腰三角形的判定;熟練掌握梯形的性質,通過作輔助線證出三角形是等腰三角形是解決問題的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:填空題
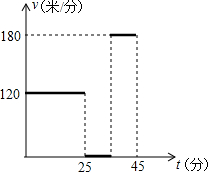 某興趣小組從學校出發騎車去植物園參觀,先經過一段上坡路后到達途中一處景點,停車10分鐘進行參觀,然后又經一段下坡路到達植物園,行程情況如圖,若他們上、下坡路速度不變,則這個興趣小組的同學按原路返回所用的時間為$\frac{95}{3}$分鐘(途中不停留)
某興趣小組從學校出發騎車去植物園參觀,先經過一段上坡路后到達途中一處景點,停車10分鐘進行參觀,然后又經一段下坡路到達植物園,行程情況如圖,若他們上、下坡路速度不變,則這個興趣小組的同學按原路返回所用的時間為$\frac{95}{3}$分鐘(途中不停留)查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4 個 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
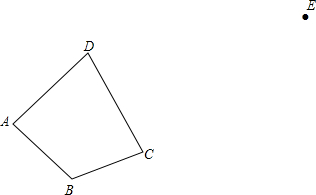 如圖,四邊形ABCD中:
如圖,四邊形ABCD中:查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 一組對邊相等,另一組對邊平行的四邊形一定是平行四邊形 | |
| B. | 對角線相等的四邊形一定是矩形 | |
| C. | 兩條對角線互相垂直的四邊形一定是正方形 | |
| D. | 兩條對角線相等且互相垂直平分的四邊形一定是正方形 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
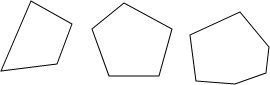 (1)四邊形不具有穩定性,要使四邊形木架不變形,至少要再釘上1根木條.
(1)四邊形不具有穩定性,要使四邊形木架不變形,至少要再釘上1根木條.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com