
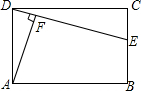
 如圖所示,在矩形ABCD中,E是BC上一點,AF⊥DE于點F.
如圖所示,在矩形ABCD中,E是BC上一點,AF⊥DE于點F.分析 (1)根據四邊形ABCD是矩形可得出∠ADC=∠C=90°,再根據相似三角形的判定定理可得出△ADF∽△DCE,由相似三角形的對應邊成比例即可得出結論;
(2)由(1)可知DF:AF=CE:DC,再結合已知條件即可求出CE的長.
解答 (1)證明:
∵四邊形ABCD是矩形,
∴∠ADC=∠C=90°,
∴∠ADF+∠CDE=90°,
∵AF⊥DE,
∴∠AFD=∠DAF+∠FDA=90°,
∴∠FAD=∠CDE,
又∵∠C=∠AFD=90°,
∴△ADF∽△DCE;
∴$\frac{DF}{CE}=\frac{AF}{DC}$,
即DF•CD=AF•CE;
(2)∵△ADF∽△DCE;
∴$\frac{DF}{CE}=\frac{AF}{DC}$,
∴$\frac{DF}{AF}=\frac{CE}{DC}$,
又∵AF=4DF,CD=12,
∴$\frac{DF}{4DF}=\frac{CE}{12}$,
∴CE=3.
點評 本題考查的是相似三角形的判定與性質以及垂直的性質和矩形的性質運用,能根據題意得出△ADF∽△DCE是解答此題的關鍵.


 金版課堂課時訓練系列答案
金版課堂課時訓練系列答案 單元全能練考卷系列答案
單元全能練考卷系列答案 新黃岡兵法密卷系列答案
新黃岡兵法密卷系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com