
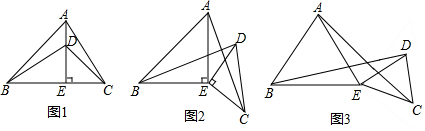
分析 (1)可以證明△BDE≌△ACE推出BD=AC,BD⊥AC.
(2)如圖2中,不發(fā)生變化.只要證明△BED≌△AEC,推出BD=AC,∠BDE=∠ACE,由∠DEC=90°,推出∠ACE+∠EOC=90°,因為∠EOC=∠DOF,所以∠BDE+∠DOF=90°,可得∠DFO=180°-90°=90°,即可證明.
(3)①如圖3中,結(jié)論:BD=AC,只要證明△BED≌△AEC即可.
②能;由△BED≌△AEC可知,∠BDE=∠ACE,推出∠DFC=180°-(∠BDE+∠EDC+∠DCF)=180°-(∠ACE+∠EDC+∠DCF)=180°-(60°+60°)=60°即可解決問題.
解答 解:(1)結(jié)論:BD=AC,BD⊥AC.
理由:延長BD交AC于F.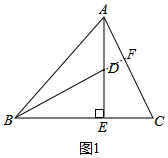
∵AE⊥CB
∴∠AEC=∠BED=90°.
在△AEC和△BED中,
$\left\{\begin{array}{l}{AE=BE}\\{∠AEC=∠BED}\\{EC=ED}\end{array}\right.$,
∴△AEC≌△BED,
∴AC=BD,∠CAE=∠EBD,
∵∠AEC=90°,
∴∠C+∠CAE=90°,
∴∠CBF+∠C=90°,
∴∠BFC=90°,
∴AC⊥BD.
(2)如圖2中,不發(fā)生變化,設(shè)DE與AC交于點O,BD與AC交于點F.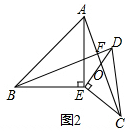
理由是:∵∠BEA=∠DEC=90°,∴∠BEA+∠AED=∠DEC+∠AED,∴∠BED=∠AEC,
在△BED和△AEC中,
$\left\{\begin{array}{l}{BE=AE}\\{∠BED=∠AEC}\\{DE=EC}\end{array}\right.$,
∴△BED≌△AEC,
∴BD=AC,∠BDE=∠ACE,
∵∠DEC=90°,
∴∠ACE+∠EOC=90°,
∵∠EOC=∠DOF,
∴∠BDE+∠DOF=90°,
∴∠DFO=180°-90°=90°,
∴BD⊥AC;
(3)①如圖3中,結(jié)論:BD=AC,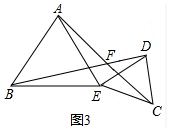
理由是:∵△ABE和△DEC是等邊三角形,
∴AE=BE,DE=EC,∠EDC=∠DCE=60°,∠BEA=∠DEC=60°,
∴∠BEA+∠AED=∠DEC+∠AED,
∴∠BED=∠AEC,
在△BED和△AEC中,
$\left\{\begin{array}{l}{BE=AE}\\{∠BED=∠AEC}\\{DE=EC}\end{array}\right.$,
∴△BED≌△AEC,
∴BD=AC.
②能;設(shè)BD與AC交于點F,由△BED≌△AEC可知,∠BDE=∠ACE,
∴∠DFC=180°-(∠BDE+∠EDC+∠DCF)=180°-(∠ACE+∠EDC+∠DCF)=180°-(60°+60°)=60°,
即BD與AC所成的銳角的度數(shù)為60°.
點評 本題考查幾何變換綜合題、等腰直角三角形的性質(zhì)、等邊三角形的性質(zhì).全等三角形的判定和性質(zhì)等知識,解題的關(guān)鍵是熟練掌握全等三角形的判定和性質(zhì),學(xué)會利用“8字型”證明角相等,屬于中考壓軸題.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數(shù)學(xué) 來源: 題型:填空題
 如圖,已知函數(shù)y=2x+b與函數(shù)y=kx-3的圖象交于點P,則關(guān)于x的不等式kx-3>2x+b的解集是x<4.
如圖,已知函數(shù)y=2x+b與函數(shù)y=kx-3的圖象交于點P,則關(guān)于x的不等式kx-3>2x+b的解集是x<4.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 3.0≤a≤3.2 | B. | 3.14≤a<3.15 | C. | 3.144≤a<3.149 | D. | 3.05≤a<3.15 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
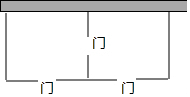 某農(nóng)場擬建兩間矩形飼養(yǎng)室,一面靠現(xiàn)有墻(墻足夠長),中間用一道墻隔開,并在如圖所示的三處各留1m寬的門.已知計劃中的材料可建墻體(不包括門)總長為21m,則能建成的飼養(yǎng)室總占地面積最大為48m2.
某農(nóng)場擬建兩間矩形飼養(yǎng)室,一面靠現(xiàn)有墻(墻足夠長),中間用一道墻隔開,并在如圖所示的三處各留1m寬的門.已知計劃中的材料可建墻體(不包括門)總長為21m,則能建成的飼養(yǎng)室總占地面積最大為48m2.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | sinA=$\frac{1}{2}$ | B. | cosA=$\frac{1}{2}$ | C. | tanA=$\frac{1}{2}$ | D. | cotA=$\frac{1}{2}$ |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com