
分析 (1)利用公式法或配方法解方程即可;
(2)設這個方程的根為x1、x2,即當x=x1,x=x2時,y=4,可設拋物線解析式y=a(2x2-x-8)+4,再將x=2,y=-4代入求a即可.
解答 解:
(1)∵2x2-x-8=0,
∴a=2,b=-1c=-8,
∴△=1+64=65>0,
∴x1=$\frac{1+\sqrt{65}}{4}$,x2=$\frac{1-\sqrt{65}}{4}$;
(2)設方程2x2-x-8=0的根為x1、x2,則
當x=x1,x=x2時,y=4,可設y=a(2x2-x-8)+4,
把x=2,y=-4代入,得-4=a(2×22-2-8)+4,
解得a=4,
所求函數為y=4(2x2-x-8)+4,
即y=8x2-4x-28.
點評 本題綜合考查了一元二次方程的根與二次函數圖象上點的坐標的關系,巧妙地設二次函數解析式,用待定系數法求解析式.


 奪冠金卷全能練考系列答案
奪冠金卷全能練考系列答案科目:初中數學 來源: 題型:解答題
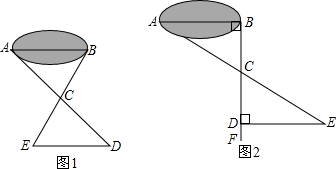 八(3)班同學到野外上數學活動課,為測量池塘兩端A、B的距離,設計了如下方案:
八(3)班同學到野外上數學活動課,為測量池塘兩端A、B的距離,設計了如下方案:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,是2016年11月月歷:
如圖,是2016年11月月歷:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com