
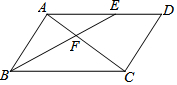
 如圖,在?ABCD中,BC=5,AB=3,BE平分∠ABC交AD于點E,交對角線AC于點F,則$\frac{{{S_{△AEF}}}}{{{S_{△CBF}}}}$=$\frac{9}{25}$.
如圖,在?ABCD中,BC=5,AB=3,BE平分∠ABC交AD于點E,交對角線AC于點F,則$\frac{{{S_{△AEF}}}}{{{S_{△CBF}}}}$=$\frac{9}{25}$. 分析 由平行四邊形的性質和BE平分∠ABC交AD于點E的條件可證明AB=AE,易證△AEF∽△CBF,利用相似三角形的性質即可求出$\frac{AF}{FC}$的值,然后由相似三角形的面積之比等于相似比的平方求得答案.
解答 解:∵四邊形ABCD是平行四邊形,
∴AD∥BC,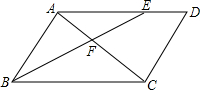
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠ABE=∠AEB,
∴AB=AE=3,
∵AD∥BC,
∴△AEF∽△CBF,
∴$\frac{AF}{FC}$=$\frac{AE}{BC}$=$\frac{3}{5}$,
∴$\frac{{{S_{△AEF}}}}{{{S_{△CBF}}}}$=($\frac{3}{5}$)2=$\frac{9}{25}$.
故答案是:$\frac{9}{25}$.
點評 本題考查了平行四邊形的性質、等腰三角形的判定和性質、角平分線的定義以及相似三角形的判定和性質,題目的難度不大,是中考常見題型.


 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 連接邊長為1的正方形對邊中點,可將一個正方形分成四個全等的小正方形,選右下角的小正方形進行第二次操作,又可將這個小正方形分成四個更小的小正方形,…重復這樣的操作,則2016次操作后右下角的小正方形面積是( )
連接邊長為1的正方形對邊中點,可將一個正方形分成四個全等的小正方形,選右下角的小正方形進行第二次操作,又可將這個小正方形分成四個更小的小正方形,…重復這樣的操作,則2016次操作后右下角的小正方形面積是( )| A. | $\frac{1}{2004}$ | B. | ${(\frac{1}{2})^{2016}}$ | C. | ${(\frac{1}{4})^{2016}}$ | D. | $1-{(\frac{1}{4})^{2016}}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com