
 如圖,△ABC中,AB=AC=10,∠BAC=30°,現將△ABC繞點A逆時針旋轉30°得到△ACD,延長AD,BC相交于點E,則DE的長是5$\sqrt{3}$-5.
如圖,△ABC中,AB=AC=10,∠BAC=30°,現將△ABC繞點A逆時針旋轉30°得到△ACD,延長AD,BC相交于點E,則DE的長是5$\sqrt{3}$-5. 分析 作CH⊥AE于H,根據等腰三角形的性質和三角形內角和定理可計算出∠ACB=$\frac{1}{2}$(180°-∠BAC)=75°,再根據旋轉的性質得AD=AB=10,∠CAD=∠BAC=30°,則利用三角形外角性質可計算出∠E=45°,接著在Rt△ACH中利用含30度的直角三角形三邊的關系得CH=$\frac{1}{2}$AC=5,AH=$\sqrt{3}$CH=5$\sqrt{3}$,所以DH=AD-AH=10-5$\sqrt{3}$,然后在Rt△CEH中利用∠E=45°得到EH=CH=5,于是可得DE=EH-DH=5$\sqrt{3}$-5.
解答 解:作CH⊥AE于H,如圖,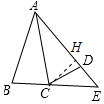
∵AB=AC=10,
∴∠B=∠ACB=$\frac{1}{2}$(180°-∠BAC)=$\frac{1}{2}$(180°-30°)=75°.
∵將△ABC繞點A逆時針旋轉,使點B落在點C處,此時點C落在點D處,
∴AD=AB=10,∠CAD=∠BAC=30°,
∵∠ACB=∠CAD+∠E,
∴∠E=75°-30°=45°.
在Rt△ACH中,∵∠CAH=30°,
∴CH=$\frac{1}{2}$AC=5,AH=$\sqrt{3}$CH=5$\sqrt{3}$,
∴DH=AD-AH=10-5$\sqrt{3}$,
在Rt△CEH中,∵∠E=45°,
∴EH=CH=5,
∴DE=EH-DH=5-(10-5$\sqrt{3}$)=5$\sqrt{3}$-5.
故答案為5$\sqrt{3}$-5.
點評 本題考查了旋轉的性質:對應點到旋轉中心的距離相等;對應點與旋轉中心所連線段的夾角等于旋轉角;旋轉前、后的圖形全等.也考查了解直角三角形,等腰三角形的性質和含30度角的直角三角形的性質.


 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案 口算與應用題卡系列答案
口算與應用題卡系列答案 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 我縣某蔬菜生產基地在氣溫較低時,用裝有恒溫系統的大棚栽培一種在自然光照且溫度為20℃的條件下生長最快的新品種.圖示是某天恒溫系統從開啟到關閉及關閉后,大棚內溫度y(℃)隨時間x(小時)變化的函數圖象,其中BC段是反比例函數y=$\frac{k}{x}$的圖象上一部分.請根據圖中信息解答下列問題:
我縣某蔬菜生產基地在氣溫較低時,用裝有恒溫系統的大棚栽培一種在自然光照且溫度為20℃的條件下生長最快的新品種.圖示是某天恒溫系統從開啟到關閉及關閉后,大棚內溫度y(℃)隨時間x(小時)變化的函數圖象,其中BC段是反比例函數y=$\frac{k}{x}$的圖象上一部分.請根據圖中信息解答下列問題:查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
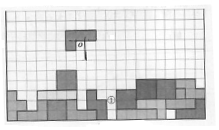 如圖,小明正在玩俄羅斯方塊,他想將正在下降的“L”型插入圖中①的位置,他需要怎樣操作?( )
如圖,小明正在玩俄羅斯方塊,他想將正在下降的“L”型插入圖中①的位置,他需要怎樣操作?( )| A. | 先繞點O逆時針旋轉90°,再向右平移3個單位,向下平移6個單位 | |
| B. | 先繞點O順時針旋轉90°,再向右平移4個單位,向下平移6個單位 | |
| C. | 先繞點O逆時針旋轉90°,再向右平移4個單位,向下平移5個單位 | |
| D. | 先繞點O順時針旋轉90°,再向右平移3個單位,向下平移6個單位 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖是二次函數y=ax2+bx+c圖象的一部分,圖象過點A(-3,0),對稱軸為直線x=-1,給出四個結論:①b2>4ac;②2a+b=0;③a+b+c=0;④若點B(-$\frac{5}{2}$,y1)、C(-$\frac{1}{2}$,y2)為函數圖象上的兩點,則y1<y2,其中正確結論是:①③④(填上序號即可)
如圖是二次函數y=ax2+bx+c圖象的一部分,圖象過點A(-3,0),對稱軸為直線x=-1,給出四個結論:①b2>4ac;②2a+b=0;③a+b+c=0;④若點B(-$\frac{5}{2}$,y1)、C(-$\frac{1}{2}$,y2)為函數圖象上的兩點,則y1<y2,其中正確結論是:①③④(填上序號即可)查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\left\{\begin{array}{l}{x=2}\\{y=6}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=6}\\{y=-2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-2}\\{y=6}\end{array}\right.$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com