
【題目】(生活觀察)甲、乙兩人買菜,甲習慣買一定質量的菜,乙習慣買一定金額的菜,兩人每次買菜的單價相同,例如:
菜價 | ||
質量 | 金額 | |
甲 |
|
|
乙 |
|
|
菜價 | ||
質量 | 金額 | |
甲 |
| ____元 |
乙 | ____千克 |
|
(1)完成上表;
(2)計算甲兩次買菜的均價和乙兩次買菜的均價.(均價![]() 總金額總質量)
總金額總質量)
(數學思考)設甲每次買質量為![]() 千克的菜,乙每次買金額為
千克的菜,乙每次買金額為![]() 元的菜,兩次的單價分別是
元的菜,兩次的單價分別是![]() 元
元![]() 千克、
千克、![]() 元
元![]() 千克,用含有
千克,用含有![]() 、
、![]() 、
、![]() 、
、![]() 的式子,分別表示出甲、乙兩次買菜的均價
的式子,分別表示出甲、乙兩次買菜的均價![]() 、
、![]() .比較
.比較![]() 、
、![]() 的大小,并說明理由.
的大小,并說明理由.
(知識遷移)某船在相距為![]() 的甲、乙兩碼頭間往返航行一次,在沒有水流時,船的速度為
的甲、乙兩碼頭間往返航行一次,在沒有水流時,船的速度為![]() 所需時間為:如果水流速度為
所需時間為:如果水流速度為![]() 時(
時(![]() ),船順水航行速度為(
),船順水航行速度為(![]() ),逆水航行速度為(
),逆水航行速度為(![]() ),所需時間為
),所需時間為![]() 請借鑒上面的研究經驗,比較
請借鑒上面的研究經驗,比較![]() 、
、![]() 的大小,并說明理由.
的大小,并說明理由.
【答案】【生活觀察】:(1)見解析表;(2)甲兩次買菜的均價是![]() 元
元![]() 千克:乙兩次買菜的均價是
千克:乙兩次買菜的均價是![]() 元
元![]() 千克;【數學思考】:當
千克;【數學思考】:當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,見解析;【知識遷移】:
,見解析;【知識遷移】:![]() ,見解析.
,見解析.
【解析】
(1)根據單價、質量與金額的關系,進行求解.(2)根據均價![]() 總金額
總金額![]() 總質量,進行求解.【數學思考】:根據均價
總質量,進行求解.【數學思考】:根據均價![]() 總金額
總金額![]() 總質量,進行表示與大小比較.【知識遷移】:根據時間=路程
總質量,進行表示與大小比較.【知識遷移】:根據時間=路程![]() 速度,進行表示與大小比較.
速度,進行表示與大小比較.
(1)根據單價、質量與金額的關系,可得甲的金額和乙的質量,如圖表所示
第二次:
菜價 | ||
質量 | 金額 | |
甲 |
|
|
乙 |
|
|
(2)根據均價![]() 總金額
總金額![]() 總質量,甲兩次買菜的均價為
總質量,甲兩次買菜的均價為![]() 元
元![]() 千克,乙兩次買菜的均價為
千克,乙兩次買菜的均價為![]() 元
元![]() 千克.
千克.
【數學思考】
:
![]() ,
,
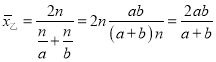 ,
,
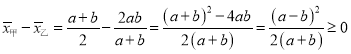 .
.
當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() .
.
【知識遷移】
:
![]() ,
,![]() ,
,
![]() ;
;
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
又![]() ,
,![]() ,
,
![]() .
.


 計算高手系列答案
計算高手系列答案科目:初中數學 來源: 題型:
【題目】小張騎自行車勻速從甲地到乙地,在途中因故停留了一段時間后,仍按原速騎行,小李騎摩托車比小張晚出發一段時間,以800米/分的速度勻速從乙地到甲地,兩人距離乙地的路程y(米)與小張出發后的時間x(分)之間的函數圖象如圖所示.
(1)求小張騎自行車的速度;
(2)求小張停留后再出發時y與x之間的函數表達式;
(3)求小張與小李相遇時x的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△OAB如圖所示放置在平面直角坐標系中,直角邊OA與x軸重合,∠OAB=90°,OA=4,AB=2,把Rt△OAB繞點O逆時針旋轉90°,點B旋轉到點C的位置,拋物線y=ax2+bx經過點C、A.

(1)求該拋物線的解析式;
(2)在x軸上方的拋物線上有一動點P,過點P作x軸的平行線交拋物線于點M,分別過點P,點M作x軸的垂線,交x軸于R、S兩點,問:四邊形PRSM的周長是否有最大值?如果有,請求出最值,并寫出解答過程;如果沒有,請說明理由.
(3)在x軸上方的拋物線上是否存在點Q,過點Q作x軸的垂線,垂足為H,使得以O、Q、H為頂點的三角形與OAB相似,如果存在,直接寫出點Q的坐標,如果不存在,請說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
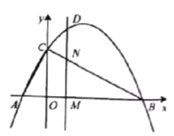
【題目】二次函數![]() 的圖象交
的圖象交![]() 軸于
軸于![]() 兩點,交
兩點,交![]() 軸于點
軸于點![]() .動點
.動點![]() 從點
從點![]() 出發,以每秒2個單位長度的速度沿
出發,以每秒2個單位長度的速度沿![]() 方向運動,過點
方向運動,過點![]() 作
作![]() 軸交直線
軸交直線![]() 于點
于點![]() ,交拋物線于點
,交拋物線于點![]() ,連接
,連接![]() .設運動的時間為
.設運動的時間為![]() 秒.
秒.
(1)求二次函數![]() 的表達式:
的表達式:
(2)連接![]() ,當
,當![]() 時,求
時,求![]() 的面積:
的面積:
(3)在直線![]() 上存在一點
上存在一點![]() ,當
,當![]() 是以
是以![]() 為直角的等腰直角三角形時,求此時點
為直角的等腰直角三角形時,求此時點![]() 的坐標;
的坐標;
(4)當![]() 時,在直線
時,在直線![]() 上存在一點
上存在一點![]() ,使得
,使得![]() ,求點
,求點![]() 的坐標
的坐標
查看答案和解析>>
科目:初中數學 來源: 題型:
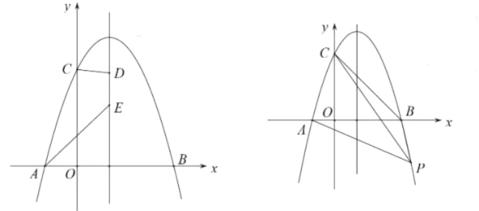
【題目】如圖所示拋物線![]() 過點
過點![]() ,點
,點![]() ,且
,且![]()
(1)求拋物線的解析式及其對稱軸;
(2)點![]() 在直線
在直線![]() 上的兩個動點,且
上的兩個動點,且![]() ,點
,點![]() 在點
在點![]() 的上方,求四邊形
的上方,求四邊形![]() 的周長的最小值;
的周長的最小值;
(3)點![]() 為拋物線上一點,連接
為拋物線上一點,連接![]() ,直線
,直線![]() 把四邊形
把四邊形![]() 的面積分為3∶5兩部分,求點
的面積分為3∶5兩部分,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
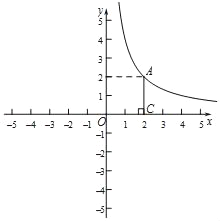
【題目】如圖,在平面直角坐標系xOy中,函數y=![]() (x>0)的圖象經過點A,作AC⊥x軸于點C.
(x>0)的圖象經過點A,作AC⊥x軸于點C.
(1)求k的值;
(2)直線y=ax+b(a≠0)圖象經過點A交x軸于點B,且OB=2AC.求a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
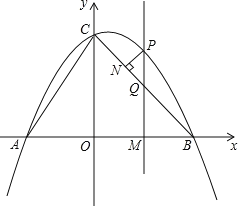
【題目】如圖,拋物線![]() 交
交![]() 軸于
軸于![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,連接
,連接![]() .點
.點![]() 是第一象限內拋物線上的一個動點,點
是第一象限內拋物線上的一個動點,點![]() 的橫坐標為
的橫坐標為![]() .
.
(1)求此拋物線的表達式;
(2)過點![]() 作
作![]() 軸,垂足為點
軸,垂足為點![]() ,
,![]() 交
交![]() 于點
于點![]() .試探究點P在運動過程中,是否存在這樣的點
.試探究點P在運動過程中,是否存在這樣的點![]() ,使得以
,使得以![]() 為頂點的三角形是等腰三角形.若存在,請求出此時點
為頂點的三角形是等腰三角形.若存在,請求出此時點![]() 的坐標,若不存在,請說明理由;
的坐標,若不存在,請說明理由;
(3)過點![]() 作
作![]() ,垂足為點
,垂足為點![]() .請用含
.請用含![]() 的代數式表示線段
的代數式表示線段![]() 的長,并求出當
的長,并求出當![]() 為何值時
為何值時![]() 有最大值,最大值是多少?
有最大值,最大值是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一臺起重機,他的機身高AC為21m,吊桿AB長為36m,吊桿與水平線的夾角∠BAD可從30°升到80°.求這臺起重機工作時,吊桿端點B離地面CE的最大高度和離機身AC的最大水平距離(結果精確到0.1m). (參考數據:sin80°≈0.98,cos80°≈0.17,tan33°≈5.67,![]() ≈1.73)
≈1.73)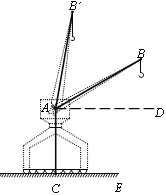
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com